I.2 1次元の力学との簡単な連成

図 I.2: 棒の伸びと接触

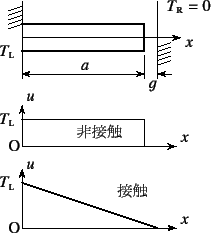
もう一つ面白い問題がある。アメリカ合州国Illinois州Evanston, Northwestern大学Dundurs教授（1980年頃）の`Elasticity'の 講義ノートにある問題である。図-I.2のように， 長さ$a$の棒の左端が温度$T\subsc{l}$になっていて， この温度を0度から徐々に上げていくことにする。 右の壁の温度は$T\subsc{r}=0$度で，$T\subsc{l}=0$の 状態での棒の右端と右の壁との間には隙間$g$があるものとする。

いわゆる1次元のHookeの法則式(3.116)に， 非弾性ひずみ（塑性ひずみと同じように^I.1扱っていい）として温度膨張ひずみを 考慮すると，Hookeの法則は

$$\sigma_{xx}=E \left(\epsilon_{xx}-\epsilon^T\right), \quad \epsilon^T(x,t)=\alpha u(x,t)$$ (I.13)

になる。ここに$\epsilon^T$は温度膨張ひずみであり，$u$は初期状態からの 温度増加分である。$E$はYoung率で$\alpha$は線膨張係数 であり，材料の定数である。 右端がまだ壁に接触する前は，棒中の温度は一様で$T\subsc{l}$に等しい。 右端が壁に接触したときには，伸び変位が$g$になったときなので， そのときの温度$T_0$は

$$\epsilon^T a=g, \quad \epsilon^T=\alpha T\subsc{l} \quad\to\quad T\subsc{l}=T_0\equiv \dfrac{g}{a \alpha}$$ (I.14)

のように求められる。

一方，$T\subsc{l}$を非常に大きな値に固定して， かつ右端が壁に接触した状態を保持し続けられた場合には， 定常状態では図-I.2の一番下のような 線形の温度分布になるだろう。したがって

$$u(x,t)=T\subsc{l}\left(1-\dfrac{x}{a}\right) \quad\to\quad \epsilon^T=\alpha T\subsc{l}\left(1-\dfrac{x}{a}\right)$$

であり，式(I.13)から

$$\epsilon_{xx}=\dfrac{\sigma_{xx}}{E} +\alpha T\subsc{l}\left(1-\dfrac{x}{a}\right)$$

となる。このとき，棒の途中には外力は存在しないので， 応力は$x$方向に一定の圧縮になるから $\sigma_{xx}=-p$とすれば

$$\epsilon_{xx}=-\dfrac{p}{E} +\alpha T\subsc{l}\left(1-\dfrac{x}{a}\right)$$

となる。この温度膨張ひずみによる棒の伸びは隙間の$g$に等しいから

$$g=\int_0^a \epsilon_{xx}\dint x =-\dfrac{p a}{E}+\dfrac{a \alpha T\subsc{l}}{2}$$

という関係が成立している。 そこで，左壁の温度を徐々に下げていき，右端が壁から離れる時点の 温度$T_1$を求めると，それは$p=0$のときに相当するので，上式から

$$\dfrac{p a}{E}=\dfrac{a \alpha T_1}{2}-g=0 \quad\to\quad T_1=\dfrac{2g}{a \alpha}=2 T_0$$ (I.15)

となり，式(I.14)の$T_0$の2倍になっていることがわかる。

この結果は面白いでしょう。つまり，では

$$T_0 < T\subsc{l} < T_1$$

の間には，一体何が起こっているのかということだ。 多分容易に想像がつくと思うが， $T\subsc{l}=T_0$で右端が接触した途端 右端の温度は0度になるから，熱伝導によって 棒はすぐに縮んで接触を失うことになる。 そこで，左壁の温度を$T_0$から$U(t)$だけ上げ続けることにして， 棒が（理想的に）右端で壁に接触して，棒に圧縮応力が生じた状態を 保持できたとすると，棒中の温度分布は一定から線形分布に徐々に変化していく。 もしそういうことが可能なら，その熱伝導問題は，$g«a$と近似できる場合

$$\D{u}{t}=\dfrac1k \D[2]{u}{x}, \quad \dfrac{p(t) a}{E}=\alpha \int_0^a u \dint x - g \ge 0, \quad 0<x<a, \quad 0<t$$ (I.16)

という問題を

$$u(0,t)=T_0+U(t), \quad u(a,t)=0, \quad u(x,0)=T_0, \qquad\mbox{ただし}\quad U(0)=0, \quad U(\infty)=T_0$$ (I.17)

の条件で解けばいい。 しかし，どんなに急に温度を上げても軸力$p(t)$は負になり， 結局右端では接触・非接触の振動が生じることになる。

「どんお」問題についての講義ノート：省略