| (C.14) |
同様に平板理論を定式化してみよう。
変位場は式(8.3) (8.4)で与えられる。
これをひずみの定義に代入すれば,式(8.5)の各成分が求められる。
再度書いておくと
| (C.14) |
および
| (C.15) |
となる。
ここでは簡単のために,![]() -
-![]() 面が平板の肉厚中心面に位置し,
厚さ
面が平板の肉厚中心面に位置し,
厚さ![]() で
で![]() ,
, ![]() に拡がる長方形平板(
に拡がる長方形平板(![]() )を対象とする。
こうすれば,仮想仕事式の体積積分や面積積分は
)を対象とする。
こうすれば,仮想仕事式の体積積分や面積積分は
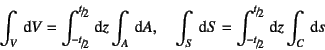
と置き直せばいいことは明らかであろう。
ただし面積積分の![]() は平板の肉厚中心面内の面積で,
は平板の肉厚中心面内の面積で,![]() は
肉厚中心面の境界周囲に沿った線座標,
ここの長方形平板なら,
は
肉厚中心面の境界周囲に沿った線座標,
ここの長方形平板なら,![]() は
は![]() か
か![]() のどちらかになる。
のどちらかになる。
まず変位場を,内力仮想仕事項に代入し,
式(8.8) (8.12)の断面力の定義を用いると
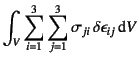 |
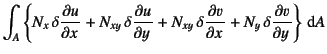 |
||
![$\displaystyle \mbox{} -\int_A \left\{
M_x \delta\D[2]{w}{x}+M_{xy} \delta\D[2...
...]{w}{x}+
M_{xy} \delta\D[2][1][x]{w}{y}+M_y \delta\D[2]{w}{y} \right\}\dint A$](s5img1062.gif) |
(C.16) |
となる。一方,分布外力仮想仕事項にも変位場を代入すれば,梁理論と同様の
表現が求められるが,ここでは式(C.7c)の![]() のような複雑な
外力を無視し,その仕事項と外力の定義を
のような複雑な
外力を無視し,その仕事項と外力の定義を
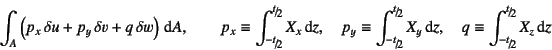 |
(C.17) |
としておく。同様に周囲の境界線上の外力仕事項は
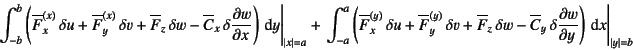 |
(C.18) |
とする。ここで上付き添え字の![]() ,
, ![]() は
それぞれ,
は
それぞれ,![]() ,
, ![]() 上での外力であることを示し
上での外力であることを示し
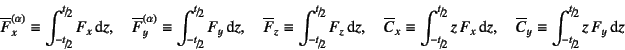 |
(C.19) |
と定義した。ここで,![]() ,
, ![]() である。
である。
まず面内の項,つまり![]() と
と![]() の項のみを取り出すと
の項のみを取り出すと
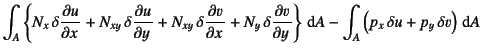 |
|||
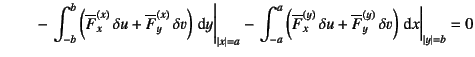 |
(C.20) |
でいい。これにGaussの発散定理(部分積分)を用いると
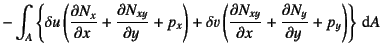 |
(C.21) | ||
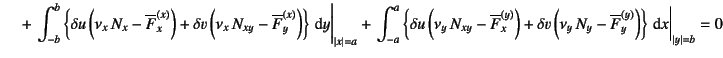 |
となる。ここに![]() は境界面の外向き法線ベクトルと
は境界面の外向き法線ベクトルと![]() の正方向との
内積の値で,
の正方向との
内積の値で,![]() で1,
で1,![]() で
で![]() の値を持つ。
同様に
の値を持つ。
同様に![]() は
は![]() で1,
で1,![]() で
で![]() の値を持つ。
この仮想仕事式の第1項から,つり合い式が
の値を持つ。
この仮想仕事式の第1項から,つり合い式が
| (C.22) |
と求められ,これは式(8.18)と一致する。境界条件は
| (C.23) | |||
| (C.24) |
となる。
次に面外曲げの項,つまり![]() に関係する項をまとめてみると
に関係する項をまとめてみると
![$\displaystyle -\int_A \left\{
M_x \delta\D[2]{w}{x}+M_{xy} \delta\D[2][1][y]{w}{x}+
M_{xy} \delta\D[2][1][x]{w}{y}+M_y \delta\D[2]{w}{y} \right\}\dint A$](s5img1088.gif) |
|||
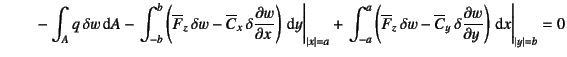 |
(C.25) |
となる。第1項にGaussの発散定理(部分積分)を用いると
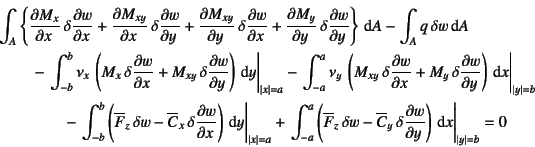
となる。再度第1項にGaussの発散定理(部分積分)を用いると
![\begin{eqnarray*}
&& - \int_A \delta w \left\{
\D[2]{M_x}{x}+\D[2][1][y]{M_{x...
...{w}{y}
\right)\dint x \right\vert _{\vert y\vert=b}=0 \nonumber
\end{eqnarray*}](s5img1091.gif)
となる。次には,第3行の下線を付した項にさらにGaussの発散定理を用いると
![\begin{eqnarray*}
&& - \int_A \delta w \left\{
\D[2]{M_x}{x}+\D[2][1][y]{M_{x...
...{w}{y}
\right)\dint x \right\vert _{\vert y\vert=b}=0 \nonumber
\end{eqnarray*}](s5img1091.gif)
という表現を得る。これを項別に整理すると
![$\displaystyle - \int_A \delta w \left\{
\D[2]{M_x}{x}+\D[2][1][y]{M_{xy}}{x}+
\D[2][1][x]{M_{xy}}{y}+\D[2]{M_y}{y} + q \right\}\dint A$](s5img1092.gif) |
|||
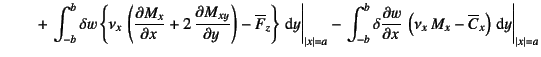 |
|||
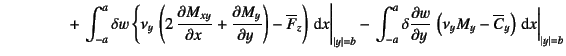 |
|||
| (C.26) |
となる。最後の下線を引いた項は,もし周囲が矩形ではなく,円板のように 滑らかな曲線を描いていれば生じない項なので,あとまわしにしよう。
この仮想仕事式が任意の仮想変位に対して成立しなければならない条件から,
まずつり合い式が
| (C.27) |
と求められ,これは式(8.21)と一致している。
境界条件も上式から誘導でき,それは次のようになる。![]() では
では
| (C.28) |
である。同様に![]() では
では
| (C.29) |
となる。これも式(8.24)と一致する。
最後に下線を引いた項であるが,これは矩形板の各角での値になっている。
例えば![]() ,
, ![]() の角の項は
の角の項は
![]() になる。
すなわち,この角で
になる。
すなわち,この角で![]() が規定されている場合には,
そこには
が規定されている場合には,
そこには![]() の大きさの支点反力が生じていることになる。
これは図-8.5で説明した隅角力である。
このように,数学(仮想仕事の原理)に頼ることによって,
特に力学的あるいは幾何学的考察をしなくても,支配方程式が
正確に定式化されていることがわかる。
の大きさの支点反力が生じていることになる。
これは図-8.5で説明した隅角力である。
このように,数学(仮想仕事の原理)に頼ることによって,
特に力学的あるいは幾何学的考察をしなくても,支配方程式が
正確に定式化されていることがわかる。