 |
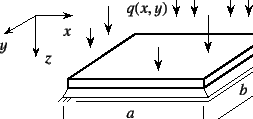
最も基本的な例として,図-8.6の4辺共に
単純支持された矩形板を解く。
任意の分布外力![]() が作用した矩形板の場合の
が作用した矩形板の場合の![]() で
表されたつり合い式は,式(8.22)で与えられている。
境界条件は式(8.24)から
で
表されたつり合い式は,式(8.22)で与えられている。
境界条件は式(8.24)から
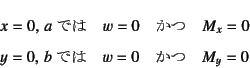
となる。力の境界条件はどちらもモーメントが作用していない
条件で,モーメントと変位の関係式(8.15)を代入すると,
例えば
![]() の辺では
の辺では
となる。しかし,この
![]() の辺上では
の辺上では![]() を
を![]() 方向にも
保持しているから
方向にも
保持しているから![]() は零である。
したがって上式の第2項は実質的に考える必要が無い。
このように考えると,たわみ
は零である。
したがって上式の第2項は実質的に考える必要が無い。
このように考えると,たわみ![]() で表した境界条件は
で表した境界条件は
と考えていい。
式(![]() )の境界条件のもとで式(8.22)の
つり合い式を解けばいいが,ここでは境界条件を満足する関数を
用いて,たわみ
)の境界条件のもとで式(8.22)の
つり合い式を解けばいいが,ここでは境界条件を満足する関数を
用いて,たわみ![]() を
を
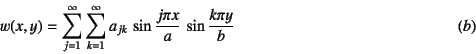
のように級数で仮定する。sine関数を選んだのは,
境界条件式(![]() )を
すべて満足するからである。節-4.7.2で
梁の振動問題を解くのに用いた固有関数法によく似ている。
(工学的に)ほとんどすべての滑らかな関数はFourier級数で
表示できることを根拠にして,2重Fourier級数
で展開したと考えてもいい。これをNavierの解法
と呼んでいる。
)を
すべて満足するからである。節-4.7.2で
梁の振動問題を解くのに用いた固有関数法によく似ている。
(工学的に)ほとんどすべての滑らかな関数はFourier級数で
表示できることを根拠にして,2重Fourier級数
で展開したと考えてもいい。これをNavierの解法
と呼んでいる。
この仮定した解(![]() )を式(8.22)の
つり合い式に代入すると
)を式(8.22)の
つり合い式に代入すると
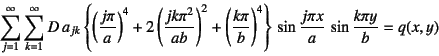
となる。この両辺に
という演算(内積あるいは仮想仕事の算定)を行おう。
このsine関数は節-4.7.2でも
示したように,例えば
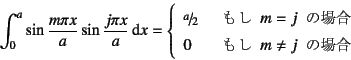
という性質(直交性)を持っている。
したがって,上の積分演算を実行すると
左辺の級数は実は![]() ,
, ![]() の場合の1項のみしか残らず,
他はすべて零になる。よって個々の
の場合の1項のみしか残らず,
他はすべて零になる。よって個々の![]() に対して
に対して
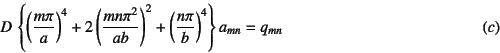
が成立しなければならない。ここに
と置いた。式(![]() )より
)より
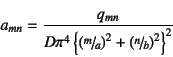
と係数を得るから,式(![]() )に代入し直せば解を得る。
結果的に
)に代入し直せば解を得る。
結果的に![]() は関数
は関数![]() の2重sine Fourier係数に相当する。
の2重sine Fourier係数に相当する。
分布外力が一様で
![]() の場合には式(
の場合には式(![]() )より
)より
となる。したがって
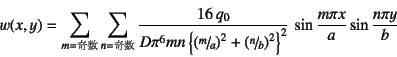
となる。図-8.7には
![]() にのみ
にのみ
のような
偏在する分布外力を作用させたときの同様の解を,特徴が
出るように誇張して示しておいた。図では![]() ,
, ![]() 共に級数の
最初の10項までで打ち切った結果を用いた。
共に級数の
最初の10項までで打ち切った結果を用いた。