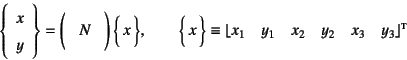• B.3.1 形状関数
• B.3.2 線形ひずみ三角形要素
• B.3.3 曲線辺をもつ要素や四辺形要素
• B.3.4 非力学問題の有限要素

B.3 高次要素や非力学問題

B.3.1 形状関数

前節の「定ひずみ三角形要素」では要素内のひずみと応力が一定になり， 解の精度はよくない。精度を上げるには通常多くの要素数が必要となる。 また境界が曲線である場合にも同様なことが必要になる。 それを改善する手段の一つに高次要素がある。 しかし，多項式の次数が上がることや要素形状が複雑になることは， 剛性行列等を求める積分を煩雑にし，そういった積分に 数値計算を用いる必要も生じてくる可能性が高い。 そういった場合には，実際の座標に代わる座標として自然座標 と呼ばれるものを用いると便利である。よく面積座標 と呼ばれるものがその一つである。 自然座標を用いると，微分や積分演算が非常に簡単にできるため 数値計算に適するが，その詳細については参考文献を参照して欲しい。

剛性行列等の積分を数値的に行うためには， 座標と節点座標との関係式が必要になる。 例えば前節の「定ひずみ三角形要素」の場合には

$$\left\{\begin{array}{c}x\ y\end{array}\right\}= \Mat{N} ... ...uad x_2\quad y_2\quad x_3\quad y_3 \right\rfloor\supersc{t}$$ (B.18)

と書け，式(B.6)と同じ表現になる。 式(B.6)が要素内任意点の変位を節点の変位成分で表した ものであることから$\mat{N}$を 変位関数と呼んだのに対し， 上式(B.18)は要素内任意点の座標値を節点の 座標値で表したものである。 したがって，この式の$\mat{N}$を形状関数 と呼ぶ。

前節の「定ひずみ三角形要素」の変位関数と 形状関数は同じ多項式で仮定されている。 このように，同じ次数の多項式で変位関数と形状関数を与える 要素をアイソパラメトリック要素 と呼んでいる。

B.3.2 線形ひずみ三角形要素

図 B.5: 線形ひずみ三角形要素の区分的多項式

近似度を上げるために用いられる高次要素の一つの例として， 要素内でひずみが線形に変化し得る三角形要素が考えられる。 この要素では変位関数に2次の多項式までを含み， 空間座標の$1$, $x$, $y$, $x^2$, $xy$, $y^2$の6項が用いられる。 したがって三角形各辺の中点にさらに三つの節点を設け， 頂点とその中点との計6点での$x$, $y$方向の変位成分を 要素自由度に用いるのが普通である。 この変位関数を図-5.4で示した区分的多項式と 同じように，節点$n$を囲む四つの三角形要素上で定義された 区分的多項式$\phi_n(x,y)$として 図示したのが図-B.5である。 対象としている平面ひずみ問題の図の範囲内任意点での変位の解が， この図の縦軸の大きさに比例していると近似している。

ただ要素形状は直線辺の三角形だから， 形状関数は式(B.18)のまま1次多項式で与えられている。 したがって，形状関数の次数が変位関数のそれより低いこと からサブパラメトリック要素 と呼ばれている。ちなみに，形状関数の 次数の方が変位関数のそれより高い要素をスーパーパラメトリック要素 と呼んでいる。具体的な表現や剛性行列等については文献を参照のこと。

B.3.3 曲線辺をもつ要素や四辺形要素

前節の要素をさらに発展させ，形状関数にも前節の変位関数と 同じ2次多項式を用いれば，曲線辺を持つ三辺高次（アイソパラ メトリック）要素が求められる。 積分は数値的に行わざるを得ないが， 具体的な数値面積積分等については別途文献を参照のこと。 また同様に，四辺形要素も上の面積座標に対応するような 自然座標を導入して定義することができる。 この場合も，数値積分で剛性行列等を算定する必要がある。

B.3.4 非力学問題の有限要素

この章に書くのは相応しくないかもしれないが，例えば拡散や浸透流の問題 であっても，その数理モデルの弱形式さえ求められれば 有限要素定式化は可能である。例えば温度や密度等の 未知関数を，図-B.2, B.5の ような区分的多項式で近似しさえすれば，その弱形式を用いた 有限要素近似が可能になるのである。 もちろん時間の要因が不可欠であり，それにまつわる 種々の問題もあるようだが，具体例は参考文献等を参照して欲しい。