• F.2.1 亀裂の変形モードと面外問題
• F.2.2 面内問題の場合
• F.2.3 平面問題の応力拡大係数

F.2 弾性亀裂と応力拡大係数

F.2.1 亀裂の変形モードと面外問題

図 F.3: 数学的亀裂の三つの変形モード

図 F.4: モードIII亀裂

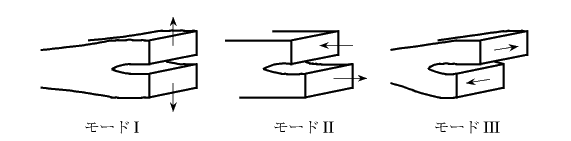
数学的亀裂は図-F.3のような三つのモードに分類される。 このうち面外変位が生じているモードIIIが最も簡単な問題になるので， まずそのような亀裂先端付近の応力状態を求めてみよう。 対象は図-F.4であり，$x$軸の負の部分に 無限に長い数学的亀裂が存在し，上半分($y>0$)が紙面手前に， 下半分($y<0$)が紙面奥に変位している状態にあるものとする。 問題の対称性と平面問題であることから

$$u\equiv 0, \quad v\equiv 0, \quad \D{w}{z}=0$$

となるので，零でないひずみは二つで

$$\epsilon_{zx}=\dfrac12 \D{w}{x}\neq 0,\quad \epsilon_{yz}=\dfrac12 \D{w}{y}\neq 0$$

だけになる。したがって，Hookeの法則から$\sigma _{zx}$と$\sigma_{yz}$， あるいは$\sigma_{rz}$と $\sigma_{\theta z}$だけが非零となる。

境界条件は，まず亀裂のある部分は自由表面なので

$$\sigma_{yz}(y=0)=\sigma_{\theta z}(y=0)=0, \quad \sigma_{yy}(y=0)=\sigma_{\theta\theta}(y=0)=0$$

であり，亀裂の無い部分は固定されているものとして$w(y=0)=0$とする。 したがって$x$軸上の境界条件は

$$w=0 \quad \mbox{along  } \theta=0, \qquad \D{w}{\theta}=0 \quad \mbox{along  } \theta=\pi$$ (F.1)

と記せばいい。 一方，物体力が無いときの極座標のつり合い式は式(J.28)から

$$\D{\left(r \sigma_{rz}\right)}{r}+\D{\sigma_{\theta z}}{\theta}=0$$

となる。またHookeの法則とひずみと変位の関係から

$$\sigma_{rz}=2\mu \epsilon_{rz}=\mu \D{w}{r}, \quad \sigma_{\theta z}=2\mu \epsilon_{\theta z}=\mu \dfrac1r \D{w}{\theta}$$ (F.2)

という関係が成立するので，上のつり合い式に代入すると，$w$で 表したつり合い式が

$$\D{}{r}\left(r \D{w}{r}\right)+\dfrac1r \D[2]{w}{\theta}=0 \quad \mbox{あるいは}\quad \nabla^2 w=0$$ (F.3)

となる。$\mu$はせん断弾性係数である。 この式(F.3)を$w$に対し， 境界条件式(F.1)を満足するように解けば， 亀裂が存在する弾性体の応力場を求めることができる。 ただ，我々は亀裂先端に大きな応力が集中する（実際には無限大になる）と 予想していて，その周辺から破壊が生じると考えているので， その先端付近の応力場にまずは興味がある。 そのため，いわゆる漸近解析 と称する解析を行うことにする。

そのために，まず解を

$$w\sim A r^p f(\theta)$$ (F.4)

のように仮定する。$\theta$方向には$\theta=0$を境にして 反対称な関数になると考えられる一方で，$r$方向については，$r=0$近傍だけを 対象とした解にしか興味が無いことから，べき乗で仮定している。 これをつり合い式(F.3)に代入して整理すると

$$p^2 r^{p-1} f+r^{p-1} f''=0$$

となる，プライムは$\theta$に関する微分を表す。つまり$f(\theta)$は

$$f''+p^2 f=0$$

を満足する関数でなければならないことから

$$f=a \sin\left(p \theta\right)+b \cos\left(p \theta\right)$$

が一般解である。これを境界条件式(F.1)，つまり

$$f(0)=0, \quad f'(\pi)=0$$

に代入すれば

$$b=0, \quad \cos\left(p \pi\right)=0$$

でなければならないことから

$$f(\theta)\sim \sin\left(p \theta\right), \quad p=\pm\dfrac12, \pm\dfrac32 \cdots$$

が解として得られる。$f$がsine関数であることから，変位$w$の$x$軸に対する 反対称性が得られている。

この結果を式(F.2) (F.4)に代入すれば

$$w=A r^p \sin\left(p \theta\right), \quad \sigma_{rz}=A \... ...igma_{\theta z}=A \mu p r^{p-1} \cos\left(p \theta\right)$$

のように，亀裂先端の変位と応力が求められる。 そこで，亀裂先端の半径$a$の領域内のひずみエネルギ$U$を求めてみると

$$U\equiv\dfrac{1}{\mu}\int_{-\pi}^{\pi}\int_0^a \dfrac12\left... ...ght) r\dint \theta\dint r =\dfrac{\pi}{2} A^2 \mu p a^{2p}$$

という表現になる。 そこで，もし 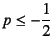$p\leq -\dfrac12$の場合には$U<0$になってしまうし， しかも領域を小さくして$a\to 0$にしたときに$U\to \infty$になる。 これは弾性論としては容認できない解を得たことになる。 このことから

$$p\ge\dfrac12 \quad\to\quad U<\infty \quad \mbox{（有界）}$$

であることがわかる。 したがって，物理的に意味のある解の漸近表現は

$$\begin{eqnarray*} w&=&w_0+A r^{\slfrac12} \sin\left(\slfrac{\theta}{2}\right)+... ...cos\left(\slfrac{\theta}{2}\right)+ O\left(r^{\slfrac12}\right) \end{eqnarray*}$$

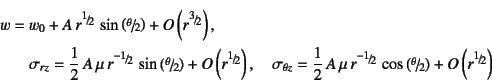
となる。 得られた結果で最も重要なのは，その応力場が

$$\sigma\sim A \mu r^{\slfrac{-1}{2}} g(\theta)$$

と表現されることである。つまり

• 亀裂先端では$r$の $\slfrac{-1}{2}$乗の特異性を 有している。$r\to 0$で無限大になる。
• 弾性係数$\mu$に比例している。
• $\theta$方向には何等かの関数になる。
• その絶対値$A$は，荷重条件や物体の形等で決まる。

と考えていいことである。 実際の物体に存在する亀裂先端で応力が無限大になることは無いから， 解が無限大になることそのものは弾性解が持つ不具合（誤差）だと捉えればいい。 しかし$r$の $\slfrac{-1}{2}$乗で分布することは， 例えば対象としている物体の「縁」から亀裂までの距離を検討するときに 重要なことであろう。 そして，絶対値$A$が荷重条件や物体形状等で決まると考えていい（漸近 解析には無限遠点での荷重条件や物体形状の影響は含まれていない）ことから， この絶対値$A$がある規準値に達したときに亀裂は進展すると 考えるのである。つまり，亀裂の破壊規準を

$$A=A\sub{cr}$$ (F.5)

と考え，この$A\sub{cr}$を破壊靭性 と呼び，これが材料の特性を表すパラメータであると考えるのである。

F.2.2 面内問題の場合

モードIとIIの場合にも同様の漸近解析が可能である。 まずつり合い式は

$$\D{\sigma_{rr}}{r}+\dfrac1r \D{\sigma_{r\theta}}{\theta} +... ...{\sigma_{\theta\theta}}{\theta} +\dfrac2r \sigma_{r\theta}=0$$

となり，Hookeの法則が

$$\sigma_{r\theta}=2\mu \epsilon_{r\theta},\quad \sigma_{rr}=... ...} +\dfrac{\kappa+1}{\kappa-1} \epsilon_{\theta\theta} \right)$$

である。ここに$\kappa$は式(3.124)と同じく

$$\kappa\equiv\left\{ \begin{array}{ll} 3-4 \nu & \quad \mbox... ...\nu}{1+\nu} & \quad \mbox{（平面応力状態）} \end{array}\right.$$

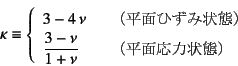
と定義される。ひずみと変位の関係は

$$\epsilon_{rr}=\D{u_r}{r}, \quad \epsilon_{\theta\theta}=\dfr... ...r \D{u_r}{\theta}+\D{u_\theta}{r}-\dfrac{u_\theta}{r} \right)$$

と定義されている。 これを

$$u_r=r^p f(\theta),\quad u_\theta=r^p g(\theta)$$

と仮定して解けば，亀裂先端の応力場を求めることができる。 必要な読者は自分で解いてみて欲しい。 別の解法としては，章-3の節-3.5.3で 応力関数を用いたものが挙げられる。図-3.24が， この面内問題の解に相当するものである。

F.2.3 平面問題の応力拡大係数

図 F.5: 無限体中の亀裂

もし無限体中に長さ$2a$の数学的亀裂が 一個だけ存在して，図-F.5の ような載荷状態にある場合の亀裂先端の応力場は

$$\left\{ \begin{array}{l} \sigma_{rr} \ \sigma_{\theta\theta... ...t\{\begin{array}{l} p(\theta) \ q(\theta) \end{array}\right\}$$

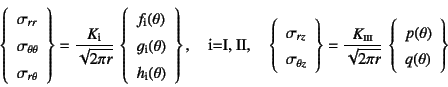
と求められる。 ここに$K\sub{i}$, (i=I, II, III)は応力拡大係数 と呼ばれ，無限体のこの境界条件下では

$$\left\{ \begin{array}{l} K\subsc{i} \ K\subsc{ii} \ K\subs... ... \sigma_{xy}^\infty \ \sigma_{yz}^\infty \end{array}\right\}$$

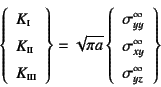
となる。 ただし，対象が無限体ではない場合や載荷条件が異なると，応力拡大係数は 異なる表現を持つ。 ルーズリーフのノートの穴が紙の端に近いことから破れ易いように感じると 思うが，それはそのような境界条件下での応力拡大係数が小さくなると 考えればいい。 いずれにしても，亀裂先端の応力の特異性は先端からの距離の平方根乗である。 そして式(F.5)と同様に，この応力拡大係数が ある規準値に達し

$$K\sub{i}={K\sub{i}}\subsc{c}, \qquad \mbox{i=I, II, III}$$

を満足したときに，亀裂が進展すると考える。 この規準値 ${K\sub{i}}\subsc{c}$を破壊靭性 と呼んでいる。

したがって，応力で表現した強度 $\sigma\sub{cr}$が 材料の規準値だけではなく亀裂の長さに依存し，その形は

$$\sigma\sub{cr}=\dfrac{{K\sub{i}}\subsc{c}}{\sqrt{\pi a}}$$ (F.6)

のようになる。 つまり，亀裂が長くなればなるほど材料強度が下がることを示している。 材料実験をしたときに，試験片の長さの平方根に反比例するような 強度・挙動が観察された場合には，亀裂の存在を疑うのがいいだろう。 また破壊靭性は温度が下がるほど小さくなることもよく知られている。 このように，材料特性に影響する要因で長さの次元を持つ パラメータを特性長さ と呼んでいる。 この式(F.6)のように材料の強度が支配されるとして， 例えば多結晶金属の強度について考察してみよう。 製鋼所で欠陥の無い材料を製造することは不可能であり， 転位が無数に内部に存在することは既に述べた。 これが載荷に伴い内部の単結晶界面に集積して，そこが空隙になったとし， その界面に沿った空隙を亀裂とみなしてみよう。 もし，そういう把握が成立するのであれば，多結晶体内に 存在するかもしれない亀裂の長さは，内部の単結晶の 粒の大きさ程度であることが容易に予想できる。 したがって，もし式(F.6)で強度が支配されるのであれば， 粒径をできるだけ小さくした方がいいことも想像できるだろう。 映像で刀鍛冶の作業を見たことがあると思うが，鋏等を作る場合にも 「鍛える」という表現で鉄槌で材料を叩いていることがわかる。 実はこれは内部の結晶粒を壊して粒径を小さくしているのである。 これによって相対的に強度を上げていると考えてもいい。 実際TMCP鋼 という製品では，圧延装置とセンサー・コンピュータを 併用して，温度処理をしながら叩くことによって高強度の厚板を製造している。 ただし溶接や切断による加熱で粒径が大きくなる可能性もあるので扱いは 難しいとされている。