- 9.5.2.1 ��b������
- 9.5.2.2 �×͊w�I���e��
- 9.5.2.3 ��--�ǂ̂悤�ɂ��ďI�Nj��x�����߂邩
- 9.5.2.4 �Ή�����ψʑ�����
- 9.5.2.5 �������C�p�̂���ޗ��̏ꍇ
�I�Ǐ�Ԑv�@��p����ꍇ�C���ۂ̋�����L���v�f�@���� �ǐՂ��Ă��̏I�Ǐ�Ԃ�\������̂́C�ޗ�����`���̊ϓ_���� ��ʂɂ͑����̍�������B ���������̌��ʂ��ǂ������Ӗ��E���x�Ő������̂��̔��f�͋ɂ߂ē���B �L���v�f�@�������܂�p�����ɁC �ŏI��Ԃ�����������x�̐��x�ŗ\�����C���S���͈̔͂� �ȕւɋ��߂邱�Ƃ��ł���C�f�ʏ����������肷��v�i�K�ł� �֗����L�Ӌ`�ł��낤�B �L���v�f�@�͂��̂��Ɨp��������B �܂�C����قnj����ɋ����\������K�v�͖����C ��r�I�e�Ղɋ��߂���悤�Ȃ荇�������邾���̉��� �w�I�ɓK���Ȃ����̏��p���Ĉ��S�����Z�肵�悤�Ƃ���̂ł���B ���ɁC���̂悤�ȉ���p���Ĉ��S���́u�ő�l�v�Ɓu�ŏ��l�v�����߂悤�Ƃ���̂��C ���̑Y����͂ł���B �����ł́C���̂悤�ȃA�v���[�`�̊�b�ɂ��ďq�ׂĂ����B �܂��͊�{�ƂȂ���J�j�Y���̑�\�Ƃ��Ă̂��ׂ�����Љ��B ���ɂ���Ɋ�Â����S���̕]���@�ɂ��Đ������悤�B �Ȃ����̐߂́CNorthwestern��w�̑�����9.35 (1980�N�������j �ɂ��`Plasticity'�̍u�`�m�[�g���Q�l�ɂ����B
�܂����J�j�Y�������f���������ł���{�I�ȍl����������B
�\����͂̏ꍇ�͂悭�Y���q���W�ƌĂ����̂����C
����ɂ��Ă͍Ō�ɉC�܂���
���ʂЂ��ݖ��ł̒莮��������B���������Ă荇������
�ƂȂ�B������![]() �͑̐ϗ͂ł���B�ޗ��͍��Y���̂Ƃ��C
�e���������C�~�����͂����ōd�����������̂Ƃ���B
������C�ޗ��̍~�����͂��I�Ǐ�Ԃł̉��͂Ƃ݂Ȃ��Ă����
�l����ƁC�|�\���̋��e���͐v�@�̂悤�Ɋ������邩������Ȃ����C
�S�f�ʂ��~�������Ԃ��I�ǂƍl����̂ŁC���e���͐v�@����
�I�ǂɋ߂���Ԃł̐v�@�ɑΉ����Ă���ƍl���Ă����B
�~��������Mises�̂���ɏ]�����̂Ƃ��邪�C
�e�������̖����Y���I���ʂЂ���
�̉���𗬂ꑥ�̎�(9.30)�ɑ�������
�͑̐ϗ͂ł���B�ޗ��͍��Y���̂Ƃ��C
�e���������C�~�����͂����ōd�����������̂Ƃ���B
������C�ޗ��̍~�����͂��I�Ǐ�Ԃł̉��͂Ƃ݂Ȃ��Ă����
�l����ƁC�|�\���̋��e���͐v�@�̂悤�Ɋ������邩������Ȃ����C
�S�f�ʂ��~�������Ԃ��I�ǂƍl����̂ŁC���e���͐v�@����
�I�ǂɋ߂���Ԃł̐v�@�ɑΉ����Ă���ƍl���Ă����B
�~��������Mises�̂���ɏ]�����̂Ƃ��邪�C
�e�������̖����Y���I���ʂЂ���
�̉���𗬂ꑥ�̎�(9.30)�ɑ�������
�Ƃ�����������������B
���̎��ƁC�e���̕��ʂЂ��݂̎�(3.110)���ׂ�ƁC
�ꌩ����![]() �ɂ����悤�Ɍ�����̂͋����[���B
�Ȃ��Ȃ�C�Y���ό`�ɂ͑̐ϕό`�������i
�ɂ����悤�Ɍ�����̂͋����[���B
�Ȃ��Ȃ�C�Y���ό`�ɂ͑̐ϕό`�������i![]() �̍ޗ������Ɠ��j
����ł���B
���̏�����(9.163)���������Ă���C
���ω��́i���̐Ð����j��
�̍ޗ������Ɠ��j
����ł���B
���̏�����(9.163)���������Ă���C
���ω��́i���̐Ð����j��
![]() ��
��
(9.164)
�ɂȂ�B���ꂩ��CMises�̍~��������
�ƂȂ�B
�������ӂ��ė~�������C���̂悤�ȑY���I���ʂЂ��ݏ�Ԃł́C
���̎����珃����f�ł�
![]() �ɂȂ���
����̂ɑ��C1��������ł�
�ɂȂ���
����̂ɑ��C1��������ł�
![]() ��
�Ȃ�̂�
��
�Ȃ�̂�
�ƂȂ�CTresca�̊W��(9.57)�̕��� �����ɂȂ��Ă��邱�Ƃɒ��ӂ���B �ΏۂƂ��Ă��镨�̂ɓK���ȑY���̈�����肵�C�����ł͍~����������������� ������̂Ƃ��āC�ȏ�̎���^����ꂽ���E�����̂��Ƃɉ����C �l�����Y����Ԃ̉������߂��邱�ƂɂȂ�B���肷��Y���̈����X �������C�ł����S�����Ⴍ�Ȃ��Ԃ����߂邱�Ƃ��ł���C���ꂪ ���̑Ώۂ̐^�̈��S���Ƃ������ƂɂȂ�B
�������C�O�߂̊�b���ɂ͂Ђ��݂ƕψʂ̊W�C�܂�^���w�I��
�x�z���������܂߂Ă��Ȃ��B
�������e����R�����Ă��邩��C�ޗ����ɂ͍~�������Ɨ��ꑥ�݂̂��܂܂��B
���������Ӗ��ł͕s�\���Ȏx�z��������
�p���Ă��邱�ƂɂȂ�B�l���悤�Ƃ��Ă���̂́C
�~�������Ƃ荇���������ł���C
���ɂ荇��������������悤�ȏ�
�i�^�̉��̕����W���j���×͊w�I���e��
�ƌĂԁB���āC������
�ƒu���ƁC����͏�ɍ~��������(9.165)������B![]() ��
��(9.164a)�Œ�`�����Ð����ł���B
��
��(9.164a)�Œ�`�����Ð����ł���B
�}-9.47�̍��Ɏ������̂́C�~������������
���͂̑g�ݍ��킹�����Mohr�̉��͉~
�ł���B���̐}������Ύ�(9.167)�������ł��邾�낤�B
���a���~������![]() �ɂȂ��Ă���B�~�̏��
�ɂȂ��Ă���B�~�̏��![]() �Ŏ�����
�ő傹��f���͂܂ł̌�����
�Ŏ�����
�ő傹��f���͂܂ł̌�����![]() �ł��邩��C������
���͏�Ԃ͐}�̉E�Ɏ������悤�Ȃ��̂ɂȂ�B
�܂�
�ł��邩��C������
���͏�Ԃ͐}�̉E�Ɏ������悤�Ȃ��̂ɂȂ�B
�܂�![]() ���Ƃ����Ȑ���
���Ƃ����Ȑ���![]() ����
����![]() �̊p�x�������ĐL�тĂ��邪�C
���̕����͐}�̉E��ɕ`�������͏�Ԑ}�ł킩��悤�ɍő傹��f���͂�
��p���Ă���ʂ̖@�������ɂȂ�B���l��
�̊p�x�������ĐL�тĂ��邪�C
���̕����͐}�̉E��ɕ`�������͏�Ԑ}�ł킩��悤�ɍő傹��f���͂�
��p���Ă���ʂ̖@�������ɂȂ�B���l��![]() ����
���l�̍ő傹��f���͂���p����ʂ̖@�������ɂȂ��Ă���B
�~����ԂƂ����̂́C
���̓�̐��̌����̂���f���͂��ő�l
����
���l�̍ő傹��f���͂���p����ʂ̖@�������ɂȂ��Ă���B
�~����ԂƂ����̂́C
���̓�̐��̌����̂���f���͂��ő�l![]() �ɂȂ��Ă��ׂ�ό`��
�\�ɂȂ��Ă����Ԃɑ�������̂ŁC���̓�̐������ׂ���ƌĂԁB
�܂�Mohr�̉��͉~�ƑΉ�������Η����ł���悤�ɁC�E�}��I, III�Ə�����
��̕������C�ő�剞��
�ɂȂ��Ă��ׂ�ό`��
�\�ɂȂ��Ă����Ԃɑ�������̂ŁC���̓�̐������ׂ���ƌĂԁB
�܂�Mohr�̉��͉~�ƑΉ�������Η����ł���悤�ɁC�E�}��I, III�Ə�����
��̕������C�ő�剞��
![]() �����
�ŏ��剞��
�����
�ŏ��剞��
![]() �̕���9.36�ɂȂ��Ă���B
���Ȃ݂ɁC�E��̐}���疾�炩�Ȃ悤�ɁC
�̕���9.36�ɂȂ��Ă���B
���Ȃ݂ɁC�E��̐}���疾�炩�Ȃ悤�ɁC![]() -
-![]() ���W�n�ł�
���W�n�ł�
�Ƃ������͏�Ԃɂ���B![]() ,
, ![]() ����������\���̂�
���Y����
����������\���̂�
���Y����![]() ,
, ![]() ��p���Ă���B���̐߂ł́C
�M���V�������̓Y�����ɂ��Ă͑��a���Ƃ�Ȃ����Ƃɂ���B
��p���Ă���B���̐߂ł́C
�M���V�������̓Y�����ɂ��Ă͑��a���Ƃ�Ȃ����Ƃɂ���B
��(9.167)�̉��͂��×͊w�I���e���
���邽�߂ɂ́C�荇����(9.162)������K�v������B
��������
�ƂȂ�B![]() ��������
��������![]() �������̍��W��
�������̍��W��![]() ,
, ![]() ���Ƃ�������
���Ƃ�������
�Ƃ������W�ϊ����ł���̂ŁC������̍��W�n�ɂ�����荇�����ɒ�����
�Ƃ����W����������B�O��![]() �������Ƃ��C���̎���
�������Ƃ��C���̎���
�ł��邱�Ƃ��Ӗ�����B�����Hencky�̒藝 �ƌĂ�Ă���B
�Ƃ���Ŏ�(9.169)�ŕ\���ꂽ�荇�����́C
�Δ����������̕��ނƂ��Ă͕����^�ɂȂ��Ă���B
���Ȃ킿�g���������Ɠ������C��̕s�A�������邢��wavefront��
�����Ƃ��ł���B���̂悤�ȕs�A�����́C������������
�����Ȑ��ƌĂ�Ă��邪�C���̋Ȑ��̕����������߂��
�ƂȂ�C���̓�̋Ȑ��͏�q��![]() ����
����![]() ���ɑ��Ȃ�Ȃ��B
���Ȃ킿�C���̋Ȑ��ɉ����đ��x�i�ψʑ����j�ɕs�A���������Ă������ꂪ�C
�����őΏۂƂ��Ă����ł���C���̓�̓����Ȑ��܂�s�A������
���ׂ���ɂȂ��Ă���B
���ɑ��Ȃ�Ȃ��B
���Ȃ킿�C���̋Ȑ��ɉ����đ��x�i�ψʑ����j�ɕs�A���������Ă������ꂪ�C
�����őΏۂƂ��Ă����ł���C���̓�̓����Ȑ��܂�s�A������
���ׂ���ɂȂ��Ă���B
��(9.171)��p���ďI�Nj��x�����߂��������
�����Ă������B�}-9.48�Ɏ������悤�ɁC
��![]() �̔̒�����
�̔̒�����![]() �̕����c���ăX���b�g��
����Ă�����̂��㉺��
�̕����c���ăX���b�g��
����Ă�����̂��㉺��![]() �ň��������ΏۂƂ���B
���w�I�T����̒e�����ŎZ�肵���������͂�Mises�̍~��������
�����~�����͂���̈�i�~������
�ň��������ΏۂƂ���B
���w�I�T����̒e�����ŎZ�肵���������͂�Mises�̍~��������
�����~�����͂���̈�i�~������![]() �ƂȂ邽�ߖ{����
���e����Ȃ��̈�j��`�����̂��C���̐}�����C�������������܂��C
�܂��Y����̎��ۂ̊g������������Ŋώ@���āC
�Ⴆ�ΐ}-9.48�̉E�}�̂悤�ȑY��������肵�悤�B
���Ȃ��_�ȉ���ł��邱�Ƃ͔ے�ł��Ȃ��B
�ƂȂ邽�ߖ{����
���e����Ȃ��̈�j��`�����̂��C���̐}�����C�������������܂��C
�܂��Y����̎��ۂ̊g������������Ŋώ@���āC
�Ⴆ�ΐ}-9.48�̉E�}�̂悤�ȑY��������肵�悤�B
���Ȃ��_�ȉ���ł��邱�Ƃ͔ے�ł��Ȃ��B
�����ɂ̓X���b�g�������Ă���̂ŁC
���R�\�ʂł���C![]() ,
, ![]() �ł���B
���������āC
�~��������(9.165)����
�ł���B
���������āC
�~��������(9.165)����
![]() �ƂȂ�B
�������COA���������k�ł���v���͖����̂ŁCOA�����͍ő�剞�͕����ɂȂ�
���Ƃ���C���̕����͐��ɂȂ�C
�ƂȂ�B
�������COA���������k�ł���v���͖����̂ŁCOA�����͍ő�剞�͕����ɂȂ�
���Ƃ���C���̕����͐��ɂȂ�C
![]() �ƂȂ�BOA������
�ő�剞�͕����ł��邱�Ƃ���C
�ő傹��f�͂�
�ƂȂ�BOA������
�ő�剞�͕����ł��邱�Ƃ���C
�ő傹��f�͂�![]() �������͎ߍ�������ƂȂ�B
�܂�
�������͎ߍ�������ƂȂ�B
�܂�
�ł���B
�����̉��͏�Ԃ̂���![]() ��
���߂���C���̍\�����x������ő��
��
���߂���C���̍\�����x������ő��![]() �����߂邱�Ƃ��ł���B
�܂�
�����߂邱�Ƃ��ł���B
�܂�![]() AOB����
AOB����![]() �����E��45�x�����ɒ����ɂȂ��Ă��āC
��`��OBC���́C�_O�𒆐S�Ƃ���~�ʏ��
�����E��45�x�����ɒ����ɂȂ��Ă��āC
��`��OBC���́C�_O�𒆐S�Ƃ���~�ʏ��![]() �����Ȃ���C
�ŏI�I��
�����Ȃ���C
�ŏI�I��![]() OCD����
OCD����![]() ���͉E��45�x�����ւ̒�����
�Ȃ�����̂Ɖ��肷��B
���������āC
���͉E��45�x�����ւ̒�����
�Ȃ�����̂Ɖ��肷��B
���������āC![]() OCD����
OCD����![]() ��
��
![]() �ɂȂ�B
�ɂȂ�B
��(9.171)�́C![]() ����
������
����
������
![]() ��
���ł��邱�Ƃ������Ă���B
���������āCOA��ł̂��̒l�ƁCOD��ł̑Ή�����l�́C
��
���ł��邱�Ƃ������Ă���B
���������āCOA��ł̂��̒l�ƁCOD��ł̑Ή�����l�́C![]() ����
���ǂ�Έ��̂܂܂ɂȂ��Ă��Ȃ���Ȃ�Ȃ��B�܂�
����
���ǂ�Έ��̂܂܂ɂȂ��Ă��Ȃ���Ȃ�Ȃ��B�܂�
�ł���B���̍��ӂɎ�(9.172)�������C
�E�ӂ�![]() ��
��
![]() �Ƃ��邱�Ƃɂ����
�Ƃ��邱�Ƃɂ����
�Ƌ��߂���B�������(9.167)�ɑ�������
�ƂȂ�B���������āC�����ʼn��肵���~���p�^�[���Ō}����
�I�Ǐ�Ԃł́C�㎮�̉��͂���![]() �̕����ɐ����Ă��邱�ƂɂȂ�B
�����āC���̑���R�͂��O��
�̕����ɐ����Ă��邱�ƂɂȂ�B
�����āC���̑���R�͂��O��![]() �Ƃ荇�����ƂɂȂ邱�Ƃ���
�Ƃ荇�����ƂɂȂ邱�Ƃ���
���ő�d�ƂȂ�B
�����ł͎�(9.166)��
�W
![]() ��p�����B
��p�����B
�������C���肷�邷�ׂ���̃p�^�[���ɂ���ĉ��͈���Ă���B �܂��×͊w�I���e��̒��ł̉��ł��邱�Ƃ���C�������ł͂Ȃ��B ��ʂɂ́C���̋Ɍ���͂̐߂ŋc�_����悤�ɁC���������� �A�v���[�`�ɂ��ő�d�͏�E��^����B �܂��p�^�[�������肷���Ƃɂ́C���Ȃ�̌o��������ώ@�̒m�����K�v�ł���B �������C�K�������A���������ׂ��������ł���Ƃ͌��炸�C �s�A���Ȃ��ׂ�������肹����Ȃ��ꍇ�����邪�C �����������ڍׂɂ��Ă͕ʓr����[79,92]�� �Q�l�ɂ��ė~�����B
�O�߂̂悤�Ȃ��ׂ�������������Ƃ��āC���ꂪ
�ǂ̂悤�ȑ����ό`��ɑΉ����Ă��邩�ɂ��čl�@���Ă������B
���W��![]() �����̕ψʑ����i���x�j��
�����̕ψʑ����i���x�j��![]() �ƋL�����Ƃɂ��C
����
�ƋL�����Ƃɂ��C
����![]() ���E
���E![]() �������̑��x��
�������̑��x��![]() ,
, ![]() �Ƃ���B
���W�ϊ�������
�Ƃ���B
���W�ϊ�������
�ł���B���͏�͎�(9.168)�ł���������C���ꑥ����
�ƂȂ�B�����ł��M���V�������̓Y�����ɂ��Ă͑��a���Ƃ�Ȃ��B
�v���C���͕������������Ă���C
���E���S�Y���̂Ȃ̂ŁC�Y���Ђ��ݑ��������̂܂ܓK���Ђ��݁i���Ђ��݁j������
��v���邱�ƂɂȂ�B���̎�����C
���Ȃ킿�C���ׂ���ɉ����ĐL�яk�݂�������ɁC���̖@�������ɂ�
�c�������Ȃ����Ƃ������Ă���C
���ׂ���ɉ����������ȑ�������f��ł��邱�Ƃ��킩��B
����f�ό`�݂̂����̐��ɉ������s�A���ɂȂ낤�Ƃ�����
�l���������B
���̍ŏ��̓�̎��ŕ\�����������C![]() -
-![]() ���W�n�̂Ђ��݂Ƃ�
���W�ϊ�����p���ĕ\���C����Ɏ�(9.21)��
�Ђ��݂Ƒ��x�̊W����p����ƁC���ꂼ��
���W�n�̂Ђ��݂Ƃ�
���W�ϊ�����p���ĕ\���C����Ɏ�(9.21)��
�Ђ��݂Ƒ��x�̊W����p����ƁC���ꂼ��
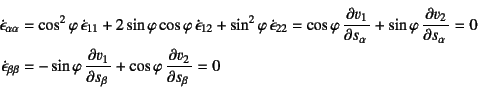
�ƂȂ�C��(9.173)�̍��W�ϊ����������邱�Ƃɂ����
�Ƃ����W����������B���̊W����Geiringer�̎� �ƌĂ�ł���B
�O�߂̗��ɂ���Geiringer�̎���p���āC�Œ���킩�邱�Ƃ��������B
����̏u�ԁCCD����
�O���͒e���̂܂���ɑ��x![]() �ŐL�т悤�Ƃ��Ă���Ƃ���B
�܂�OD�����͋��E�����Ƃ��ē����Ȃ��Ƃ���B���̏��������ɂ��āC
���肵��
�ŐL�т悤�Ƃ��Ă���Ƃ���B
�܂�OD�����͋��E�����Ƃ��ē����Ȃ��Ƃ���B���̏��������ɂ��āC
���肵��![]() ���E
���E![]() ���ɉ�����Geiringer�̎��̓�����
�ǐՂ��邱�Ƃɂ���āC
�Ⴆ��OA�����̎ߍ��������𐳂Ƃ���
���x
���ɉ�����Geiringer�̎��̓�����
�ǐՂ��邱�Ƃɂ���āC
�Ⴆ��OA�����̎ߍ��������𐳂Ƃ���
���x![]() ��
��
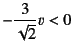 �ƂȂ�C
�X���b�g�������J�����Ƃ��Ă��邱�Ƃ��炢�͂킩��悤���B
�ڍׂ͕ʓr����[79,92]���Q�l�ɂ��ė~�����B
�ƂȂ�C
�X���b�g�������J�����Ƃ��Ă��邱�Ƃ��炢�͂킩��悤���B
�ڍׂ͕ʓr����[79,92]���Q�l�ɂ��ė~�����B
���č����̂悤�ɁC������������C�p������ޗ��̏ꍇ���C
���l�̉�͂����ďI�Nj��x�����߂邱�Ƃ�����B
���̂悤�ȍޗ��́C��-9.4.2�ł�
�������悤�ɁCMises�̍~�������̂悤�Ȃ��̂ł͂Ȃ��C
���ω��͂��֗^����Mohr-Coulomb�̔j��K��
�ŏI�Ǐ�Ԃ��}����ƍl���邱�Ƃ������B�S����
��![]() �Ƃ��C�������C�p
��
�Ƃ��C�������C�p
��![]() �Ƃ����Ƃ��C���̔j��K����
�Ƃ����Ƃ��C���̔j��K����
�ŗ^������B�����ɁC![]() �́C
�@���x�N�g����
�́C
�@���x�N�g����
![]() �Ƃ���ő傹��f���͖ʏ��
����f���͂ł���C
�Ƃ���ő傹��f���͖ʏ��
����f���͂ł���C![]() �͂��̖ʂ̖@�������́u���k�v
������
�͂��̖ʂ̖@�������́u���k�v
������![]() �ł���B
�������C�p��
�ł���B
�������C�p��![]() ��
��![]() ���̌�����
���̌�����![]() �Ƃ��������Ȃ����ƁB
�Ƃ��������Ȃ����ƁB
Mises�̏������g��Ȃ����C�}-9.47��Mohr��
���͉~��p���ĉ��͏�Ԃ�\�����邱�Ƃ͂ł���B������
�ƒu����
�Ƃ����W�͐�������B�������C![]() �͎�(9.164a)�Œ�`����
�Ð����ł���B�܂�
�͎�(9.164a)�Œ�`����
�Ð����ł���B�܂�![]() �́C
�ő�剞�͕����ł���C�}-9.47��
�́C
�ő�剞�͕����ł���C�}-9.47��
![]() ��
��������B��(9.176)�̍��ӂ��ő�ɂ���悤�Ȗ�(
��
��������B��(9.176)�̍��ӂ��ő�ɂ���悤�Ȗ�(![]() )�̌�����
)�̌�����
�ŗ^������B���������āC�j���Ԃɂ����ẮC
��(9.178)�Ǝ�(9.164b) (9.177)��
�p���Ĕj��K���̎�(9.176)������������
�ɂȂ�B����C��(9.178)���荇����(9.162)�ɑ�����C
���̓����Ȑ��i�s�A�����j�����߂��
�ƂȂ�B���̓�{��![]() ����
����![]() ���ł���B
�������C�p�̉e���ŁC���̓�{�͒������Ȃ��Ȃ��Ă���B
�ȏ�̊W�����ׂĂ荇�����ɑ������ƁC�����
���ł���B
�������C�p�̉e���ŁC���̓�{�͒������Ȃ��Ȃ��Ă���B
�ȏ�̊W�����ׂĂ荇�����ɑ������ƁC�����
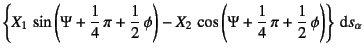 |
|||
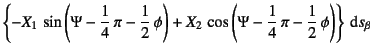 |
(9.182) |
�Ə������Ƃ��ł��CKötter�̎�
�ƌĂ�Ă���B![]() ����̂Ƃ��ɂ͎�(9.171)��Hencky�̎���
��v����B
����̂Ƃ��ɂ͎�(9.171)��Hencky�̎���
��v����B
����ɁC���ׂ����ŁC�������C�p�������ꍇ�Ɠ��l�ɏ�����
����f�ό`���������Ȃ��ꍇ�ɂ́C��(9.175)��Geiringer��
���ɑ�������W��
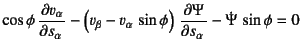 |
|||
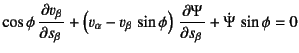 |
(9.183) |
�ƂȂ�B�������C�����̂悤�ȍޗ��̏ꍇ�ɂ́C���ׂ�����
����f�݂̂Ȃ炸�C�c���i�_�C���^���V�[
�j��������̂����ʂł���B
�܂�C�Ⴆ���ׂ����̑Y���I�ȕό`���x�̐ڐ�����������
���������̔䂪�_�C���^���V�[�p�x![]() ���Ȃ��C
���Ȃ��C![]() �ŕ\�����Ƃ���B
�����������ꍇ�̏㎮�ɑ�������W�������߂��Ă��邪�C
����ɁC���̂��ׂ�����_�ɑΉ�����3�����̍\���������߂�ƁC
����͐�-9.4.3�Ŏ��������̑Y�����f����
���ʂȏꍇ�ɑ������邱�Ƃ��킩���Ă���B
�܂莮(9.147)�̃p�����[�^
�ŕ\�����Ƃ���B
�����������ꍇ�̏㎮�ɑ�������W�������߂��Ă��邪�C
����ɁC���̂��ׂ�����_�ɑΉ�����3�����̍\���������߂�ƁC
����͐�-9.4.3�Ŏ��������̑Y�����f����
���ʂȏꍇ�ɑ������邱�Ƃ��킩���Ă���B
�܂莮(9.147)�̃p�����[�^![]() ,
, ![]() ,
, ![]() ,
, ![]() ��
��
�ƂȂ��Ă���B�����d�����܂߂Ă��Ȃ�����![]() �ƂȂ��Ă����
�v����B�����[���̂�
�ƂȂ��Ă����
�v����B�����[���̂�![]() �����ɂȂ��Ă���[54]���Ƃł���B
�ڍׂɂ��Ă͕���[52,53,54,68]���Q��9.37�̂��ƁB
�����ɂȂ��Ă���[54]���Ƃł���B
�ڍׂɂ��Ă͕���[52,53,54,68]���Q��9.37�̂��ƁB
�y�ؕ���ł̋�̗��}-9.49�� �������B���͌ÓT�I�Ȗ��ł��邪�C�������ݖ��ƌĂ����̂ł���B �Ⴆ�Β��ڊ�b�����̒�R�͂̕]���̃��f���ƍl��������B �}�������̂͒�����Prandtl�̂��ׂ���p�^�[���ł��邪�C ���̃p�^�[��[34]����Ă���Ă���B�B ������l���[112]�ł������悤�ȃp�^�[���������B �E�Ɏ������̂́C���f�w����̑͐ύ��n�Ղɔ������邸��ό`�� �n�\�̕ό`���V�~�����[�V�����������̗̂�ł���B ���f�w�̊p�x�ɂ���邪�C�}�̂悤�Ȏ啛�̓�̂��ׂ肪 ��������[90,112]���Ƃ��킩���Ă���B �Ⴆ�Δ��d�^�[�r�����i�[����{�݂́C�^�[�r���̈��S�ғ��̊ϓ_���� ���̏��̌X����������x���ɋK�������B ���̂悤�Ȓn�\�ʂ̕ό`�̗\���ɂ��C���̂悤�Ȃ��ׂ�����_���g����B
�����ŏ����l�������ɂ߁C��(9.174)��
���_�Ɋ�Â����Ǐ��������ό`
�̑��݂�����[34]���Ă݂悤�B
���̌��_����́C����f�ό`���Ǐ����������ׂ���́C
���̐��ɉ����ĐL�т������悤�ȕs�A�������ƒ�`�������邱�ƂɂȂ�B
���邢�́C���̐��̖@�������ɂ�
�L�тȂ��s�A�������ƍl���邱�Ƃ��ł��邾�낤�B
�܂莮(9.174)����C
![]() ����
����
����
����
![]() �ƂȂ�悤�Ȑ������ׂ���ł����
�݂Ȃ��̂ł���B�}-9.50�̂悤�ɍ��W����ݒ肵�C
���܁C
�ƂȂ�悤�Ȑ������ׂ���ł����
�݂Ȃ��̂ł���B�}-9.50�̂悤�ɍ��W����ݒ肵�C
���܁C![]() �����ɒ����~����̈����莎���Ђ�
���̕�����
�����ɒ����~����̈����莎���Ђ�
���̕�����![]() �ň�l�Ɉ������Ă���Ƃ���B
���̂Ƃ��ɔ������邹��f�т�
�ň�l�Ɉ������Ă���Ƃ���B
���̂Ƃ��ɔ������邹��f�т�![]() ������
������![]() ��
��![]() �����ɐL�т�Ƃ���B
����ƁC��q�̏����͑O�߂Ɠ��l��
�����ɐL�т�Ƃ���B
����ƁC��q�̏����͑O�߂Ɠ��l��
�ƂȂ�B���͏�Ԃ�
![]() �����ő��̐����͗�Ȃ̂ŁC
�����͂��v�Z���ė��ꑥ�ɑ�������
�����ő��̐����͗�Ȃ̂ŁC
�����͂��v�Z���ė��ꑥ�ɑ�������
�Ƃ����Ђ��ݑ����������Ă��邱�ƂɂȂ�B������㎮�ɑ�������
�Ƃ����p�x��B
�����I�ȍő傹��f���͂̌����i45�x�j�ɂȂ��Ă��Ȃ����Ƃ͋����[���B
���̂悤�Ȃ��ׂ���������������Ȃ��玎���Ђ̒f�ʂ��ׂ��Ȃ��Ă����i�i��j
�ƍl�����Ă���B
���͕���[34]��Hill�́C����ʂЂ��ݏ�Ԃ̂���f�т̌�����
�q�ׂĂ��邪�C
����͏㎮(![]() )���i�Y���I�j���ʂЂ��ݏ�Ԃœ����Ă��邩��ł���B
)���i�Y���I�j���ʂЂ��ݏ�Ԃœ����Ă��邩��ł���B
�ł́C��(9.163)�̂悤�ȑY���I���ʂЂ��݂���������ꍇ���l���āC
��q�̂悤�ȉ��͂�1����Ԃɂ���Ƃ����
�ƂȂ�B����𗬂ꑥ�ɑ�������
�Ƃ����Ђ��ݑ����������Ă��邱�ƂɂȂ�B
����ď�q�̂Ђ��ݑ����̍��W�ϊ����Ƃ��ׂ���̒�`�����
| (9.185) |
�Ƃ�������B
���̉��͏�ԂŊ�����![]() -
-![]() �ʓ��œ��l�̊��
���������߂�ƁC
�ʓ��œ��l�̊��
���������߂�ƁC
![]() �Ȃ̂�
�Ȃ̂�
| (9.186) |
�Ƃ�����������B �����}�������̂��}-9.51�ł���B ���S�Y���̂ƊȒP�Ȃ��ׂ���̒�`�Ɋ�Â����\���ł͂��邪�C ���ƂȂ������Ƃ��炵���Ƃ��낪�������B
���āC�n�Սޗ��̂悤�ȑY���I�Ȗc��������ޗ��̂���f�є����ɂ��Ă�
���l�̉�͂��\���낤���B
�����ɐ�-9.4.2�ŏЉ���Y�����f����p���Ă݂�B
��(9.133a)�̗��ꑥ��p���Ď�(9.163)���Y���I
���ʂЂ���
�����ɑ�������
�ƂȂ�B
![]() �Ɖ��肵
�Ɖ��肵
�ƒ�`[42]�����
�Ǝ�(9.187)�ŕ\�����
�����͐����́C
![]() �̒�`����
��ɖ�������B
�̒�`����
��ɖ�������B![]() �̏ꍇ���C
�O�߂̕��ʂЂ��݂̏ꍇ�̉��͏�ԂɈ�v����B
�̏ꍇ���C
�O�߂̕��ʂЂ��݂̏ꍇ�̉��͏�ԂɈ�v����B
���ă_�C���^���V�[������̂�����C
���ׂ����ł��P���Ȃ��ׂ�ł͂Ȃ��C���ׂ���̖@�������ւ̖c����
�����ɋN����ƍl������B
�����������ł́C�ߎ��I�ɑO�߂̎�(![]() )�̂���f�т̔����K����
����������̂Ƃ��āC���̌����ׂĂ݂悤�B
������2���ډ�Ԃ��l����
)�̂���f�т̔����K����
����������̂Ƃ��āC���̌����ׂĂ݂悤�B
������2���ډ�Ԃ��l����![]() �Ƃ���B
��(9.188) (9.189)����(
�Ƃ���B
��(9.188) (9.189)����(![]() )�ɑ�������
)�ɑ�������
�ƂȂ�B�\-9.8�����̌��ʂł���B45�x�� ����90�x���ꂽ��̕��������݂���悤�ɂȂ�B �P���������̕��ʂЂ��݈����莎���ł��C�K�������ډו�������45�x�� �����ɂ��ׂ�����o��Ƃ͌���Ȃ��Ƃ�����������[4]������B �܂��C����S�y��3�������ɂ����Ĕ������邹��f�т̌����́C �ǂ��炩�Ƃ����ƍډו�������45�x���������������ɂȂ� ��������[143]������C �\�̊p�x�̕Е�������ɑ������Ă���悤�Ɍ�����B �Ƃ���őO�߂ł�1���ډ�Ԃ̂悤�ɂ��ĎZ�肵�Ă������C ���̐߂̗U����������炩�Ȃ悤�ɁC2���ډׂ̉��͔�Ɉˑ����� ����f�т̌�������ӂɌ��܂錋�ʂɂȂ������Ƃ͋����[���C �Ƃ��������C�ǂ����ςł���B
�O�߂œ����������ׂ���Ƃ������J�j�Y�������������Ƃ��āC
���̏u�Ԃ̊O�͂̍ő�l���������T���o�����@���ȉ��ɐ�������B
����Ɋ�Â��Ĉ��S���͈̔͂�]�����悤�Ƃ���̂ł���B
�Ȃ������Ő�������̂́C
���z���쓙�Ŏg���Ă����ۗL�����ϗ�
�̕]���@�̊�b�ł���C��������⋴�r�̓��l�ۗ̕L�����ϗ͂̊�b�I��
�l�����ł���B
�ΏۂƂ���ޗ��͒e�E���S�Y���̂ł���Ƃ���B����������
�ƕ����ł���Ƃ���B������![]() �͕ψʑ����i���x�j�ł���C
�Y�����̃R���}�͎��̎w�W�������Ɨ��ϐ��Ŕ������邱�Ƃ��Ӗ�����B
���̂Ƃ��e��������Hooke�̖@��
�͕ψʑ����i���x�j�ł���C
�Y�����̃R���}�͎��̎w�W�������Ɨ��ϐ��Ŕ������邱�Ƃ��Ӗ�����B
���̂Ƃ��e��������Hooke�̖@��
�����C�Y��������Prandtl-Reuss�̗��ꑥ����
�̂悤�ɑ̐ϕό`�͔������Ȃ����̂Ƃ���B
�܂��~����Mises�̍~������
�ɏ]�����̂Ƃ���B
�܂�����Ƃ��āC���ɂ͒e���I�ȑ̐ϕό`�������Ȃ����̂Ƃ���B
�����ό`���_�Ȃ̂ŁC
�荇�����́C���͂��̂��̂���т��̑����ɂ��Ă������`�ŕ\�������̂Ƃ�
�ƂȂ邱�Ƃɂ���B
������![]() �͑̐ϗ͂ł���B���E�����́C�\�ʂ̂�����
�͑̐ϗ͂ł���B���E�����́C�\�ʂ̂�����![]() ��
�ψʂ��K�肳��Ă���C
��
�ψʂ��K�肳��Ă���C![]() �̕����ŊO�͂Ƃ��̑�����
�̕����ŊO�͂Ƃ��̑�����
�ŗ^��������̂Ƃ���B
�����ɁC![]() �͋��E�\�ʂ̊O�����@���P�ʃx�N�g���ł���C
�͋��E�\�ʂ̊O�����@���P�ʃx�N�g���ł���C![]() ��
�\�ʊO�͂ł���B
��
�\�ʊO�͂ł���B
��`: �����i�Y������j �Ƃ́C���̏������ɖ��������Ԃł���B
�������� ��(9.26)�Œ�`�����ݐϑY���Ђ��݂ł���B
�܂�C����̏u�Ԃɂ͊O�͂̕ω��������܂܁C��t�ȑY���Ђ��ݑ����݂̂� �������悤�Ƃ��Ă�����̂Ƃ���̂ł���B ���傤�ǒe���̕���������C�O�͂̕ω��������܂܈قȂ�ό`�p�^�[���ւ� ����ł���u�Ԃł���̂ɑΉ����Ă���B���̂Ƃ�
�藝: ���ɂ�
����������B
�ؖ�: ���̂悤�Ȑϕ����l����ƁC ��(9.191)�`��(9.195)��p�����
�ƂȂ�B�͕����͂ł���B ����CMises�̍~�������� ����������
�ł��邱�Ƃ� �����Ă���̂ŁC�㎮�̔�ϕ����̑�2���͗�ł���B ����������
�ł���ȏ�
�Ƃ��������������ƂɂȂ�B �����(9.191)��Gauss�̔��U�藝��p����C���̎��̍��ӂ�
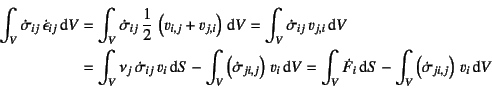
�Ƃ��\�����Ƃ��ł��邪�C ��(9.196)�̂荇�����Ǝ�(9.198)�̕���̒�`���� �㎮�̐ϕ��̒l�͗�ɂȂ�B���������Đ��l�ł��鎮(9.200)�� �E�ӂ͗�ł������蓾��
����������B�����2���`���ł���C�͐��̒萔�ł��邱�Ƃ���C ���̓��ł͕���
����������B�܂��C��(9.195)��Hooke�̖@������
���������邱�Ƃ���C���̒藝�͏ؖ��ł����B
���������āC��(9.192) (9.195) (9.202)����
�n: ���ɂ�
����������B
�܂�C���ɂ͒e���ό`�͈�ؐ����Ȃ����ƂɂȂ�B �\���͊w�I�ɏ������������ȕ\�������Ă����ƁC ���ɂ͑Y���ό`�����ӏ��ɏW�����C ����ȊO�̉ӏ��ł͒e�����ׂ̂��߂ɂقƂ�Ǖό`�������Ȃ�C �\���S�̂�����ƍl��������B
�����ŁC��̏���`����B��͐×͊w�I���e���
��`: �×͊w�I���e���� �����������̂Ƃ���B
�����ɊO��![]() ,
, ![]() �͈��̐v�d�̂悤�Ȃ��̂�
�l���C����ɏ悶�Ă���
�͈��̐v�d�̂悤�Ȃ��̂�
�l���C����ɏ悶�Ă���![]() �͈��S���̂悤�Ȃ��́C���邢�͕���d��
�v�d�̔�̂悤�Ȃ��̂ł���B������͉^���w�I���e���
�͈��S���̂悤�Ȃ��́C���邢�͕���d��
�v�d�̔�̂悤�Ȃ��̂ł���B������͉^���w�I���e���
��`: �^���w�I���e���� �����������̂Ƃ���B
���̂Ƃ��C���S����
�ŗ^������B�������� �^���w�I���e��ɂ�����ݐϑY���Ђ���
�ł���C�͕��̓��̂��ׂ���i�ʁj�̏W���ł���B �����
�́C���̂��ׂ����́u����v�ʁC �܂���̐ڐ������̂��ׂ�̌����̑��x�̕s�A���ʂł���B
���̂悤�ȓ�̏���l�����Ƃ�
�藝: �^�̕���d���v�d���{�C
,
�� ����Ƃ����
����������B
���ꂪ��E���E�藝�ƌĂ����̂ł���B �܂�C�L���v�f�@����p�����ɎZ��ł���s���S�����͊w�I�ɈӖ��̂��� ��̏�ƁC�O�߂̂��ׂ�̃��J�j�Y���Ƃ�p���āC ���S���͈̔͂����߂���Ƃ������̂ł���B ���͈̔͂�������ΗL���v�f�@���͐v�i�K�ł͕s�v�ɂȂ邩������Ȃ��B
�ؖ�(): ��(9.58)��Drucker�� �����̈�̌`���Ƃ��āC�����̉��͏�Ɛ×͊w�I���e��̊Ԃɂ�
����������B�e�����Y�����̐ϕό`�͕��ɂ͐����Ă��Ȃ����Ƃ� ��(9.191)��p�����
�ƂȂ�B����Ɏ�(9.204)���l�����Ēe���Ђ��ݑ������������C ����Ɏ�(9.191)���������
�ƂȂ�̂ŁCGauss�̔��U�藝��p������ł荇�������l������ƁC ���ǎ�(9.209)��
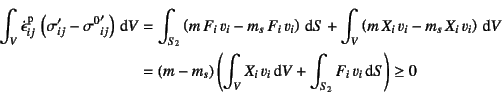
�ƂȂ�B���ɂ͊O�͎͂d�����悤�Ƃ��邽�߁C,
�ł��邱�Ƃ���
�� �ؖ��ł����B
�ؖ�(): ��̏ؖ��̎�(9.209)�����3�s�� ���l�̉��Z�������
�ƂȂ�B�������͐^�̕��̉��͂ł���B ���̓��ɑ��x�̕s�A����
�����邱�Ƃ��l����Gauss�� ���U�藝��p�����
�ƂȂ�B��������
�͂��ׂ��
���͂��ޕ��̂̓�ʂł���C ���R
�Ȃ̂�
�ƂȂ邪�C���̖@�������̑��x�͘A�����Ă���C�s�A���Ȃ̂͐��� �ڐ������̑��x�����ł���B�܂����̐ڐ������̉��͂́C���ׂ�����_���� �~�����͂ɒB���Ă���̂ŁC����
�ƂȂ�B����C���̍��ӂ�
�ł���B�����^���w�I���e��̑Y���Ђ��ݑ����������̉��͏�� �����ł���C�Y���Ђ��ݑ����Ɖ��͂̋������i���ꑥ�j�̓����� �\����(9.34)���������邪�C ���̓�̏�͈�v���Ă��Ȃ��̂ŁC�Œ���� �Ȃ���Ȃ炸�C����������
�ƂȂ�B���̉��͍͂~�����������Ă��镔�������邩��C����
�̕s��������������B���̎��̍��ӂ���(9.210)�̉E�ӂŒu���������
�ƂȂ邱�Ƃ���
��B��(9.206)�ʼn^���w�I���e�ꂪ����O�͎d���͐��� ��`�����̂ŁC��(9.207)�̒�`��p����ƁC ���̎��������ؖ��ł����B �����������������E�E�E
�Ⴆ�ΐ}-9.52�̂悤�ȃm�b�`�̂����
�����苭�x�ׂ悤�B![]() �ɑ��ẮC
�}�̒����ɂ���悤�Ƀm�b�`���ӂ̍ޗ��͖������āCA, B, B', C��
�̈�Ő�߂�ޗ��ŋߎ�����B�����āC���̗̈�ɁC
�s�A�������܂ނ��ׂ��
�ɑ��ẮC
�}�̒����ɂ���悤�Ƀm�b�`���ӂ̍ޗ��͖������āCA, B, B', C��
�̈�Ő�߂�ޗ��ŋߎ�����B�����āC���̗̈�ɁC
�s�A�������܂ނ��ׂ��![]() ,
, ![]() ����`�����Ƃɂ���āC
�����
����`�����Ƃɂ���āC
�����
��
![]() �x
�Ƌ��߂���B���������āC�͂̂荇�����
�x
�Ƌ��߂���B���������āC�͂̂荇�����
�ƂȂ�B
���![]() �ɂ��ẮC�}�̉E�ɂ���悤��PQ�i
�ɂ��ẮC�}�̉E�ɂ���悤��PQ�i![]() ���ׂ���j��
������
���ׂ���j��
������![]() �̕s�A�����x��������Ƃ�����ŁC
����ȊO�̕����͍��̂̂܂܂ƍl����B�����������x��́C
�^���w�I���e��̈�ɂȂ��Ă���̂ŁC
���������(9.207)�ɑ�������
�̕s�A�����x��������Ƃ�����ŁC
����ȊO�̕����͍��̂̂܂܂ƍl����B�����������x��́C
�^���w�I���e��̈�ɂȂ��Ă���̂ŁC
���������(9.207)�ɑ�������
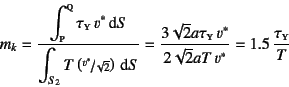
�ƎZ��ł���B���������āC�㉺�E��
�Ƌ��߂���B���������ނȂ�
��(9.166)����
![]() ��
�x�����邩��C������͏��������Ƃ����炩�ł���B
���̑��̗�͕���[92]�����Q�Ƃ̂��ƁB
��
�x�����邩��C������͏��������Ƃ����炩�ł���B
���̑��̗�͕���[92]�����Q�Ƃ̂��ƁB
�����ŗU�����ꂽ��@����╽�ɓ��Ă͂߂Ă݂悤�B �\�����ނ̏ꍇ�ɂ́C�f�ʂ����ׂč~�������ꍇ�ɁC �������u�W���I�ȁi�����̖����Ȃ����j���ׂ���v�Ƃ��ă��f��������B ���̂悤�Ȓf�ʂ��Y���q���W �ɂȂ����Ə̂����B���̏ꍇ�Ő������悤�B ���́C�ޗ����e�E���S�Y���̂ł����Ă��C ���{�����Ƃ��Ă�Bernoulli-Euler�̉���͐������Ă�����̂Ƃ���B ���������āC�Ђ��݂͏�ɐ��`���z������B���ɂ͋Ȃ��݂̂� ��p���Ă���ƍl���Ă���̂ŁC�Ȃ��ɂ���Đ��������͂���鎲�͂� ��ɂȂ�悤�ɒ���������`����Ă���ƍl���Ă������B ���K���4-1��2�Ԃ� �������t�O�p�`�f�ʂ��ɂ��āC�f�ʂ��~�����Ă����l���������B
�Ȃ�����p����ƁC�}-9.53��(a)�Ɏ������悤�ɁC
�������������(
![]() )�ɂ��邽�߂ɁC
��ɍ~������̂͒f�ʉ��[�ł���B
���̏�Ԃ̒�R���[�����g
)�ɂ��邽�߂ɁC
��ɍ~������̂͒f�ʉ��[�ł���B
���̏�Ԃ̒�R���[�����g![]() ���~�����[�����g
�ƌĂԁB
����ɋȂ�����p������ƁC�e�E���S�Y���̂Ȃ̂Ő}��(b)�Ɏ������悤�ɁC
�f�ʉ�����
���~�����[�����g
�ƌĂԁB
����ɋȂ�����p������ƁC�e�E���S�Y���̂Ȃ̂Ő}��(b)�Ɏ������悤�ɁC
�f�ʉ�����
![]() �̕����̖ʐς������Ă����Ƌ��ɁC
���͂���ɂȂ�悤�ɉ��͗�̎��͂�����Ɉړ����Ă����B
����ɋȂ����i�ނƒf�ʏ�[���~�����C�}��(c)�̂悤�ɂȂ�B
���̂Ƃ�
�̕����̖ʐς������Ă����Ƌ��ɁC
���͂���ɂȂ�悤�ɉ��͗�̎��͂�����Ɉړ����Ă����B
����ɋȂ����i�ނƒf�ʏ�[���~�����C�}��(c)�̂悤�ɂȂ�B
���̂Ƃ�
![]() �ł���B
����ɋɒ[�ȏ�Ԃɂ܂ŋȂ����i�݁C�f�ʓ��ɂ͒e�������������Ȃ�悤��
�Ɍ����l�����̂��}��(d)�ł���C��������̒f�ʂ̏I�Ǐ�Ԃƍl����B
���̂Ƃ�
�ł���B
����ɋɒ[�ȏ�Ԃɂ܂ŋȂ����i�݁C�f�ʓ��ɂ͒e�������������Ȃ�悤��
�Ɍ����l�����̂��}��(d)�ł���C��������̒f�ʂ̏I�Ǐ�Ԃƍl����B
���̂Ƃ�
![]() �ł���C����
��Ԃ̒�R���[�����g
�ł���C����
��Ԃ̒�R���[�����g![]() ���S�Y�����[�����g
�ƌĂԁB����ȏ�̊O�͂ɂ͂�����R���ł��Ȃ��Ȃ�̂ŁC
���̒f�ʂ̓q���W�ɂȂ����̂Ɠ����ŁC�܂�Ȃ��邵���Ȃ��Ȃ�ƍl����̂ł���B
���̎O�p�`�f�ʂ̏ꍇ�ɂ�
���S�Y�����[�����g
�ƌĂԁB����ȏ�̊O�͂ɂ͂�����R���ł��Ȃ��Ȃ�̂ŁC
���̒f�ʂ̓q���W�ɂȂ����̂Ɠ����ŁC�܂�Ȃ��邵���Ȃ��Ȃ�ƍl����̂ł���B
���̎O�p�`�f�ʂ̏ꍇ�ɂ�
�ƂȂ�B���̒f�ʌW��![]() ���Y���f�ʌW��
�ƌĂ�Ă���B
����
���Y���f�ʌW��
�ƌĂ�Ă���B
����![]() �̒����`�f�ʂ̏ꍇ��
�̒����`�f�ʂ̏ꍇ��
![]() �ł���B
��X�̒f�ʂ̑Y���f�ʌW���͕���[114]���Q�Ƃ̂��ƁB
�ł���B
��X�̒f�ʂ̑Y���f�ʌW���͕���[114]���Q�Ƃ̂��ƁB
�}-9.54�ɂ���悤�ȁC
����![]() ��
��![]() �̕���4�Ӌ��P���x������C
�����z�d
�̕���4�Ӌ��P���x������C
�����z�d![]() ���ڂ��Ă���ꍇ���Ɏ�낤�B
�ŏ��͐×͊w�I���e����l����B
���ڂ��Ă���ꍇ���Ɏ�낤�B
�ŏ��͐×͊w�I���e����l����B![]() �{�̉d���������ꍇ��
���̋Ȃ��Ɋւ���荇�����͎�(8.21)�C�܂�
�{�̉d���������ꍇ��
���̋Ȃ��Ɋւ���荇�����͎�(8.21)�C�܂�
�ŗ^������B�~���������Ȃ����[�����g�ŏ�����Ă�������]�܂����̂ŁC
�}�̒����ɂ���悤�ɁC�S�Y�����[�����g�̂Ƃ��̉��͕��z��z�肵�āC
�����S�ʂ����Ɉ�l�ȉ��͕��z�����肵�āC
��(8.12)�̒�`��p�����
�Ƌߎ�����B����ʉ��͂�Mises�̍~�������ɑ�������
�ŋߎ��ł���B�荇�����Ƌ��E���������郂�[�����g�̉��̈��
�ł���B���̃��[�����g���z�͔̒����ōő�ɂȂ�̂ŁC���̒�����
��̍~����������������Ă���Ƃ���ƁC�������
��B����![]() ��O�̎���
��O�̎���![]() �Ɠ��l���邱�Ƃɂ���Ĉ��S��
�Ɠ��l���邱�Ƃɂ���Ĉ��S��![]() ��
��
�̂悤�ɋ��߂���B
����C�^���w�I���e��Ƃ��ẮC���E�����Ƃ���݂Ƌȗ��̊W������
����ݑ���![]() �Ƃ���
�Ƃ���
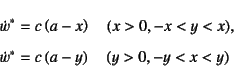
�Ɖ��肵�悤�B�܂�C�}�̉E�[�Ɏ������悤�ɁC
�e�p����L�т�~��̑Ίp����ɂ̂ݑY���q���W���������C
���̂܂܋t���܂̎O�p������ɂ���ނƂ������̂ł���B
���̂���ݑ����ɑ��ẮC�Y���q���W�̕����ȊO�͏��ׂ��ꂽ
��ԂɂȂ��Ă���̂ŁC�Ђ��݂͖����B
���邢�́C��Œ�`��������݂���͋ȗ��i����݂�2�K���W���j����ł��邽�߁C
�Ђ��݂������ƍl��������B
���������āC��(9.207)��![]() �̕��q�̑�1���͖����Ȃ�
�̕��q�̑�1���͖����Ȃ�
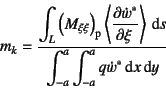
�ƒ�`�����������B![]() �́~��̑Y���q���W�̐��ɑΉ����C
���̐ϕ��́C���̐��ɉ��������W
�́~��̑Y���q���W�̐��ɑΉ����C
���̐ϕ��́C���̐��ɉ��������W![]() �ɑ��ēK�p������̂Ƃ���B
�܂�
�ɑ��ēK�p������̂Ƃ���B
�܂�
![]() �̓q���W�����܂����s�A���ʂł��邪�C
���肵������ݑ�������
�̓q���W�����܂����s�A���ʂł��邪�C
���肵������ݑ�������
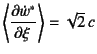 �ł��邱�ƂƁC��(
�ł��邱�ƂƁC��(![]() )����
)����
![]() ��
�u���������Ƃ���
��
�u���������Ƃ���
�ƎZ��ł���B
�����ł͎�(9.166)�̊W
![]() ��p�����B����C�����
��p�����B����C�����
�ł����B���ǁC����2�����
�ƂȂ�B���������ď㉺�E��
�Ƃ����͈͂ŗ}����ꂽ���ƂɂȂ�B
�W������f�O��![]() �ƏW���O�̓��[�����g
�ƏW���O�̓��[�����g![]() ����p���C
���z�d
����p���C
���z�d![]() ����p���Ă�����̏ꍇ���l���悤�B
�܂��×͊w�I���e��
��
����p���Ă�����̏ꍇ���l���悤�B
�܂��×͊w�I���e��
��
�Ƃ����Ȃ����[�����g�̏�![]() �ł���B
�����Ƀv���C����
�ł���B
�����Ƀv���C����![]() �Ɋւ��������\���C
�Ɋւ��������\���C![]() ��
��(9.211)�Œ�`�����悤�ȑS�Y�����[�����g�ł���B
��
��(9.211)�Œ�`�����悤�ȑS�Y�����[�����g�ł���B![]() ��
��(4.24)�Œ�`���ꂽ�L���ł���B
����C�^���w�I���e��
��
��
��(4.24)�Œ�`���ꂽ�L���ł���B
����C�^���w�I���e��
��
�Ƃ�������ݑ����̏�![]() �ł���B
�ł���B
![]() ��
�Ή�����^���w�I���e�Ȃ���݊p�ł���B
���̂Ƃ���(9.207)�̈��S��
��
�Ή�����^���w�I���e�Ȃ���݊p�ł���B
���̂Ƃ���(9.207)�̈��S��![]() ��
��
�ŗ^������B
��(9.207)�̕��q�̑�1���������̂́C���̗�Ŏ����悤�ɁC
���ׂ���C�܂�Y���q���W��}�������ӏ��ȊO�͂��ׂď��ׂ����
�e����ԁi���m�ɂ͖����͏�ԁj�ɂȂ��Ă����
���邩��ł���B![]() �͑Y���q���W�̉ӏ��Ń��J�j�Y����
�^���w�I���e��Ƃ���d�������ł���C
�͑Y���q���W�̉ӏ��Ń��J�j�Y����
�^���w�I���e��Ƃ���d�������ł���C![]() ��
�^���w�I���e��ƊO�͂�����d�������ł���B
��
�^���w�I���e��ƊO�͂�����d�������ł���B
��Ƃ��Đ}-9.55�Ɏ���������![]() ��
��l��1���s�Ò�����l���悤�B
�W���d�̓X�p�������ɍ�p���Ă���B�Ȃ����[�����g�}����
���炩�Ȃ悤�ɁC�d�𑝂₵�Ă����C�܂��Œ�[��
��
��l��1���s�Ò�����l���悤�B
�W���d�̓X�p�������ɍ�p���Ă���B�Ȃ����[�����g�}����
���炩�Ȃ悤�ɁC�d�𑝂₵�Ă����C�܂��Œ�[��![]() �ɒB����
�����ɑY���q���W���������邾�낤�B���������̒i�K�ł͂܂��Ò�\��
�i�P���x�����ɏ������\���j�Ȃ̂ŁC
����ŕ���ɂ͎���Ȃ��B����ɉd�𑝂₷���Ƃɂ���āC
���ɂ̓X�p�������̋Ȃ����[�����g��
�ɒB����
�����ɑY���q���W���������邾�낤�B���������̒i�K�ł͂܂��Ò�\��
�i�P���x�����ɏ������\���j�Ȃ̂ŁC
����ŕ���ɂ͎���Ȃ��B����ɉd�𑝂₷���Ƃɂ���āC
���ɂ̓X�p�������̋Ȃ����[�����g��![]() �ɒB���C
�����ɂ��Y���q���W����������B
����ŕs����ɂȂ�Y������Ɏ���ƍl����̂ł���B
�ɒB���C
�����ɂ��Y���q���W����������B
����ŕs����ɂȂ�Y������Ɏ���ƍl����̂ł���B
�×͊w�I���e��́C���[�ƃX�p�������̋Ȃ����[�����g��![]() �ɒB����
�͂��荇���Ă����Ԃł���B
����͐}-9.56��
�ɒB����
�͂��荇���Ă����Ԃł���B
����͐}-9.56��![]() �̃��[�����g�}�̂悤�ɂȂ�C
�荇�����Ƃ��
�̃��[�����g�}�̂悤�ɂȂ�C
�荇�����Ƃ��
�ł����B�O�Ԗڂ̎��́C���[�����g�}�̃X�p���������E����
�X�����E�[�̂���f�͂ɓ������Ƃ������̂ł���B���ꂩ��
�ƂȂ邱�Ƃ���
| (9.215) |
�����߂���B���̂Ƃ��C�ǂ̂悤�ɂ���ނ��ɂ��Ă͖��Ȃ��̂� �×͊w�I���e��ł���B �~�������Ƃ荇�����E�͂̋��E�����݂̂��������̎����S�����B
���ɉ^���w�I���e��́C![]() �̋Ȃ����[�����g�}�ɑΉ�����
����ݏ�Ԃ���C�}-9.56�̉��̐}�̂悤��
����ݏ�ԂɓˑR�ω������Ƃ��čl��������B
�܂�C���[�ƃX�p�������͑Y���q���W�ɂȂ���̂́C
�̋Ȃ����[�����g�}�ɑΉ�����
����ݏ�Ԃ���C�}-9.56�̉��̐}�̂悤��
����ݏ�ԂɓˑR�ω������Ƃ��čl��������B
�܂�C���[�ƃX�p�������͑Y���q���W�ɂȂ���̂́C![]() ��
��R���Ǐ��I�Ɏ����āi�}�ł͂����ɉ�]�o�l��}�����Ď������j�����
�l����̂ł���B�q���W���ȊO�͂��ׂď��ׂ��Ă܂������ɂȂ�ƍl����̂ŁC
�����ɂ͋Ȃ����[�����g�͕��z�����C�͂̂荇���͖��Ȃ��ł������ƂɂȂ�B
���������ĉ^���w�I���e��́C
�}�������悤�Ȑ܂����̂���݂ւ̕ω��̏�ɂȂ�ƍl��������̂ŁC
���[�ƃX�p�������ɋ��e��̕s�A���ʂ�
���ꂼ��
��
��R���Ǐ��I�Ɏ����āi�}�ł͂����ɉ�]�o�l��}�����Ď������j�����
�l����̂ł���B�q���W���ȊO�͂��ׂď��ׂ��Ă܂������ɂȂ�ƍl����̂ŁC
�����ɂ͋Ȃ����[�����g�͕��z�����C�͂̂荇���͖��Ȃ��ł������ƂɂȂ�B
���������ĉ^���w�I���e��́C
�}�������悤�Ȑ܂����̂���݂ւ̕ω��̏�ɂȂ�ƍl��������̂ŁC
���[�ƃX�p�������ɋ��e��̕s�A���ʂ�
���ꂼ��
![]() ,
,
![]() ����
��������B���ꂩ�烁�J�j�Y���̎d��������
����
��������B���ꂩ�烁�J�j�Y���̎d��������
![]() �ł���C
�O�͂̎d��������
�ł���C
�O�͂̎d��������
![]() �ƂȂ�B
����C�w�I�ȊW����
�ƂȂ�B
����C�w�I�ȊW����
 ����������̂�
����������̂�
| (9.216) |
�Ƌ��߂���B�ȏ�̉�͂���
�ƂȂ�B���Ȃ킿�㉺�E����v�������Ƃ���C�u�^�́v�������߂�ꂽ���̂� ���߂���Ă���B�{������?
���̗�̂悤�ɁC�㉺�E����v����̂́i��X�ɂ́j�ςɎv����B
�Ƃ����̂��C��E�͘A���̂Ƃ��Ă̂荇�����j����u�Ԃ�����ł���B
����͒u���Ă����C�\���͊w����ɂ�����Ɍ���͂ł́C
�荇���ƍ~�������������ʼn\�ȑY���q���W�̔z�u�̒�����C
�ŏ��̏�E��^������[�h�ɂ���āC���S�������߂�̂��嗬�ł���B
����́C�×͊w�I���e��ɐ�������^���ꂪ�C�^���w�I�ɂ����e�ꂾ����ł���B
��`���[�����ŗᎦ�����̂��}-9.57�ł���B
�����͗�������![]() �ŁC�f�ʂ���l�Ƃ��C
�}�̍��[�̂悤�ȋ��E�����E�d�����Ƃ���B
�����}�ɋȂ����[�����g���z���������B
���������āC�Y���q���W����������\���������̂́C�}��
�����Ɏ������悤�Ȏ��ӏ��ł���B���̃��[������3���̕s�Ò�ł��邽�߁C
�Y���q���W���l�ӏ��ɔ����������_�őY������B
�����ł��낢��ȑg�ݍ��킹�őY���q���W�̏ꏊ�����߁C
���̂Ƃ��ɋȂ����[�����g�}���������������邩�ǂ����i�荇����
�������邩�ǂ����j���m�F������ŁC��E�藝��
�ŁC�f�ʂ���l�Ƃ��C
�}�̍��[�̂悤�ȋ��E�����E�d�����Ƃ���B
�����}�ɋȂ����[�����g���z���������B
���������āC�Y���q���W����������\���������̂́C�}��
�����Ɏ������悤�Ȏ��ӏ��ł���B���̃��[������3���̕s�Ò�ł��邽�߁C
�Y���q���W���l�ӏ��ɔ����������_�őY������B
�����ł��낢��ȑg�ݍ��킹�őY���q���W�̏ꏊ�����߁C
���̂Ƃ��ɋȂ����[�����g�}���������������邩�ǂ����i�荇����
�������邩�ǂ����j���m�F������ŁC��E�藝��![]() �����߂�B
���߂�ꂽ
�����߂�B
���߂�ꂽ![]() �̂����C�ł����������l��^���郁�J�j�Y����
���߂������[�h�Ƃ������ƂɂȂ�B���ꂪ�}�̉E�[�̃��[�h9.38�ł���C���̂Ƃ�
�̂����C�ł����������l��^���郁�J�j�Y����
���߂������[�h�Ƃ������ƂɂȂ�B���ꂪ�}�̉E�[�̃��[�h9.38�ł���C���̂Ƃ�
 �ɂȂ�B
��̓I�ȋ��ߕ���
���̑��̗�ɂ��Ă͕���[79]�����Q�Ƃ̂��ƁB
�ɂȂ�B
��̓I�ȋ��ߕ���
���̑��̗�ɂ��Ă͕���[79]�����Q�Ƃ̂��ƁB
�O�߂̗���ȕ֖@�̗�̂悤�ȁC�㉺�E����v��������������舵���Ă������B
�܂��C�}-9.13�̗��[�P���x������3�_�Ȃ���
�㉺�E�藝�ōl���Ă݂悤�B
���̏ꍇ�͐}-9.58�̂悤�ȃ��J�j�Y�����l�����
�����̂ŁC�܂��荇������
�ƂȂ�B����C�d�����l�����
����i`0'�̓Y�����͏ȗ������j
�̂悤�Ɉ�v����B���������̏I�ljd![]() �̒l�́C
�S�Ђ��ݗ��_�ŗ�����ǐՂ���
���߂�ꂽ�I�ljd�̎�(9.20)��
�̒l�́C
�S�Ђ��ݗ��_�ŗ�����ǐՂ���
���߂�ꂽ�I�ljd�̎�(9.20)��![]() �Ƃ���v����B
�܂�C�\���n�̏ꍇ�ɂ͉^���w�I���e��Ɛ×͊w�I���e��̗�������
��������悤�ȏ�����߂邱�Ƃ��\�Ȃ̂ŁC
���̂悤�ɏ㉺�E����v���邪�C
�ǎ҂͂��ꂪ�^�����ƐM���邱�Ƃ��ł��邾�낤���B
����f�ʂ��~���������ƑS�Y�����[�����g�ɒB����܂ŁC�����̍ޗ��ɂ�
��ؑ����������Ȃ��Ƃ������Ƃɋ^��͊����Ȃ����낤���B
�Ƃ���v����B
�܂�C�\���n�̏ꍇ�ɂ͉^���w�I���e��Ɛ×͊w�I���e��̗�������
��������悤�ȏ�����߂邱�Ƃ��\�Ȃ̂ŁC
���̂悤�ɏ㉺�E����v���邪�C
�ǎ҂͂��ꂪ�^�����ƐM���邱�Ƃ��ł��邾�낤���B
����f�ʂ��~���������ƑS�Y�����[�����g�ɒB����܂ŁC�����̍ޗ��ɂ�
��ؑ����������Ȃ��Ƃ������Ƃɋ^��͊����Ȃ����낤���B
�ł́C�d�������z�d�̏ꍇ�͂ǂ����낤�B�}-9.59�̂悤�ɁC
�Ώ̌n�ł����ɁC�Ȃ����[�����g�����������z�ł��邱�Ƃɒ��ӂ����������C
�͂̂荇�������
�ƂȂ�B�܂��d����
�ƂȂ邱�Ƃ���
�̂悤�ɁC���̏ꍇ����v����B
�Ō�ɕ���[81]�ɂ��闼�[�Œ���ɓ����z�d����p�����ꍇ��
�ΏۂƂ��悤�B
���̏ꍇ���}-9.60�̂悤�ɍl��������B
�܂��C�Ώ̌n�ŋȂ����[�����g�����������z�ł��邱�Ƃ���C
�荇������
�ƂȂ�B�܂��d����
�ƂȂ邱�Ƃ���
�̂悤�Ɉ�v����B
���ĐÒ�\���n�̏ꍇ�́C�}-9.14��
���̒e�Y��������ǐՂ����Ƃ��̂悤�ɁC
����f�ʂ��Y���q���W�ɂȂ�܂łɒf�ʂ��������Ȃ��Ă��܂��悤��
�傫�ȑ����������邱�Ƃ���������C
���̋Ɍ���͂œ�����![]() �̃��x���܂Œ�R���������邾�낤�B
�������C�}-9.55��}-9.60��
�悤�ȕs�Ò�\���n�ŁC�����ӏ�����s���đS�Y�����[�����g��Ԃ�
��������C���̒f�ʂ��S�Y�����[�����g��ԂɎ���܂ŁC����
��s�����f�ʂ����S�Ȃ܂܂ł��������ǂ����ɂ��ẮC
�^������ǎ҂̕��������Ǝv���̂����C�ǂ����낤�B
���Ƃ��ƁC���ʂЂ��ݏ�Ԃ̑Y����́E�Ɍ���͂ɂ����ẮC
�I�����ꂽ�I�Ǐ�ԁi�ݒ肵��
�̃��x���܂Œ�R���������邾�낤�B
�������C�}-9.55��}-9.60��
�悤�ȕs�Ò�\���n�ŁC�����ӏ�����s���đS�Y�����[�����g��Ԃ�
��������C���̒f�ʂ��S�Y�����[�����g��ԂɎ���܂ŁC����
��s�����f�ʂ����S�Ȃ܂܂ł��������ǂ����ɂ��ẮC
�^������ǎ҂̕��������Ǝv���̂����C�ǂ����낤�B
���Ƃ��ƁC���ʂЂ��ݏ�Ԃ̑Y����́E�Ɍ���͂ɂ����ẮC
�I�����ꂽ�I�Ǐ�ԁi�ݒ肵��![]() ,
, ![]() ���ׂ�n��
�Y���q���W�̈ʒu�j�̈Ⴂ�ɂ���ĈقȂ���E�d�̌W��
���ׂ�n��
�Y���q���W�̈ʒu�j�̈Ⴂ�ɂ���ĈقȂ���E�d�̌W��![]() ��B
�㉺�E�藝�͂��̌W���͈̔͂������Ă���邩��C���S���m�ۂ̂��߂ɂ�
�ł��邾�����E�ɂ�����E�d���Q�l�ɂ��Đv����������Ƃ�
�������Ă���悤�ɂ��v����B
�������C���̐߂ł��Ꭶ�����\���n�̏ꍇ�ɂ͏㉺�E�����݂����C
���肵�����J�j�Y���ɑ��Ĉ���������o�Ă��Ă��Ȃ��B
���̓����^�����Ɩ��ꂽ�Ƃ��C���͋t�ɁC���肵���I�Ǐ�ԂɈˑ�����
��̉\�����o�������Ƃ͍l�����Ȃ����낤���B
�����������Ƃ���ƁC���E�d�����߂�ɂ́C��͂��X�̏I�Ǐ�Ԃ�
�ł��邾�������������Ȃ���Ȃ�Ȃ��C�Ƃ������ƂɂȂ�B
��B
�㉺�E�藝�͂��̌W���͈̔͂������Ă���邩��C���S���m�ۂ̂��߂ɂ�
�ł��邾�����E�ɂ�����E�d���Q�l�ɂ��Đv����������Ƃ�
�������Ă���悤�ɂ��v����B
�������C���̐߂ł��Ꭶ�����\���n�̏ꍇ�ɂ͏㉺�E�����݂����C
���肵�����J�j�Y���ɑ��Ĉ���������o�Ă��Ă��Ȃ��B
���̓����^�����Ɩ��ꂽ�Ƃ��C���͋t�ɁC���肵���I�Ǐ�ԂɈˑ�����
��̉\�����o�������Ƃ͍l�����Ȃ����낤���B
�����������Ƃ���ƁC���E�d�����߂�ɂ́C��͂��X�̏I�Ǐ�Ԃ�
�ł��邾�������������Ȃ���Ȃ�Ȃ��C�Ƃ������ƂɂȂ�B
���Ďʐ^-9.61��9�K���Ă� �^�������C2011�N3��11��14��46���̃}�O�j�`���[�h9�ő�k�x7�Ƃ��� ���k�n�������m���n�k�Ŏ���Q�̈�ł���B �ꏊ�͂��̌����̊p�ŁC2�K�̉���܂�3�K���ʂ̒���ł���B ����4�����ɂ���Ɠ����ȏ�̔�Q�����B ��Ќ�3���ڂȂ̂ŗ]�k�ɂ�鑹����������Ă͂��邪�C ����Ƃ��܂�Ⴂ�͖����C �Ɛ��ޗ��̃R���N���[�g���قƂ�ǔ��������ēS�̂� �ɂȂ��Ă���B���������f�ʌ����́w�����x��ڂɂ���ƁC �S�f�ʍ~�����Ă��܂����f�ʂ��C���̑S�Y�����[�����g���u�ێ��v���� ��R���Ă��邱�Ƃ��ƂĂ��w�^���x�Ƃ͎v���Ȃ��̂ł͂Ȃ����낤���B
�|�̏ꍇ�ɂ͐x�����������߁C�~���������ƁC���Ȃ�傫�ȕό`��Ԃ܂�
�T������炸�ɑS�Y�����[�����g�Œ�R�ł������ł���B
���̂��߁C�Ⴆ�ΐ}-9.55��1���s�Ò���̏ꍇ���C
�����̌Œ�[�������~�����C���̌�S�Y�����[�����g�ɒB�������Ƃ��C
���̂܂܌p�����Ē�R�ł���Ƃ��Ă���B���̌��ʁC
�I�ljd����(9.217)�̂悤�ɋ��߂邱�Ƃ��ł��C
����![]() �̒l��
�̒l��
�ƂȂ��Ă���B �������|�\���̏ꍇ���C��ό`�ɔ����ėn�ڕ����Ǐ��I�ɔj�铙���āC �f�ʌ����Ɠ����̑����������邱�Ƃ����Ă��邾�낤�B
�����ŁC���̋Ɍ���͂̌��ʂ𗿗����邽�߂ɁC���̕s�Ò���̍��[��
�~���������Ƃ̏��������Ă݂悤�B
�ȒP�̂��߂ɁC���̐߂ł͋�`�f�ʗ���ΏۂƂ���̂�
�Ƃ����W��������̂Ƃ���B
�܂����[�������~������̂͋Ȃ����[�����g�}����
�ł���B���̌�C���[���S�Y�����[�����g�ɒB�������ƒ�����
�����~������̂́C��͂�Ȃ����[�����g�}����
�ɂȂ�B��(9.221)�Ɣ�r���Ă����炩�Ȃ悤��
![]() �ł��邩��C�}-9.62�̉E�オ���
�Ȑ��̂悤�ɁC�I�Ǐ�Ԃ܂ʼnd�͒P���ɑ������邱�ƂɂȂ�B
�������C����͍��[���S�Y�����[�����g���ێ��ł��邱�Ƃ�O��Ƃ��Ă���B
�ł��邩��C�}-9.62�̉E�オ���
�Ȑ��̂悤�ɁC�I�Ǐ�Ԃ܂ʼnd�͒P���ɑ������邱�ƂɂȂ�B
�������C����͍��[���S�Y�����[�����g���ێ��ł��邱�Ƃ�O��Ƃ��Ă���B
�����ŏ�̎ʐ^-9.61�̂悤�ȏ�z������ƁC
���̗��̍��[�̍ޗ��͎���ɑ傫�ȑ������C�f�ʌ�����������\���͍����B
�����������Ƃ���ƁC�I�Ǐ�Ԃł͍��[��
��R���[�����g�͗�ɂȂ��Ă��܂���������Ȃ��B
�܂肻�̏I�Ǐ�Ԃ́C�O�߂̗��[�P���x�����̏I�Ǐ�Ԃƈ�v���邱�ƂɂȂ�B
���������āC�I�Ǐ�Ԃ�![]() �̒l�͎�(9.218)��
�̒l�͎�(9.218)��![]() �ɂȂ�B
�����l����ƁC�}-9.62��A�̗����̂悤�ɁC
���[��
�ɂȂ�B
�����l����ƁC�}-9.62��A�̗����̂悤�ɁC
���[��![]() �ɂ͒B�������̂́C����������ɑ�������
��R���������Ȃ�C����
�ɂ͒B�������̂́C����������ɑ�������
��R���������Ȃ�C����![]() �ɂ͒B���邱�ƂȂ��C
�ɂ͒B���邱�ƂȂ��C![]() ��
�d���x���ɂ܂ŗ����Ă��܂����Ƃ��\�z�����B
����
��
�d���x���ɂ܂ŗ����Ă��܂����Ƃ��\�z�����B
����![]() �̃��x��9.39���c�����x
�ƌĂԂ��Ƃɂ���B
�̃��x��9.39���c�����x
�ƌĂԂ��Ƃɂ���B
�ł͂��̗�ŁC![]() ,
, ![]() ,
, ![]() ,
, ![]() ��
�ǂ̃��x���Őv���s���ׂ����낤���B
��
�ǂ̃��x���Őv���s���ׂ����낤���B
���������āC���S�����\���Ɋm�ۂ���C���s�̐v�͓K���ƍl������B
���������c�����x��![]() ��
��![]() ��菬�����ꍇ�ɂ�
�Y�܂����Ƃ���ł��낤�B
��菬�����ꍇ�ɂ�
�Y�܂����Ƃ���ł��낤�B
�ł͈��S���m�ۂ̂��߂ɁC![]() �Őv����̂��D�܂����ƌ����邾�낤���B
�Őv����̂��D�܂����ƌ����邾�낤���B
�^�d�͉�Ђ��^���d���œd�C�ݔ��̐v������Ă��܂����̂́C ���̌o�ϐ������S�������D�悵�����Ƃ���̌������낤�B ������Ƃ����āC��͂�c�����x�Őv���ׂ����ƒf���ł��邾�낤���B �ƂĂ�������ł���B ������u�z��v�Ƃ����ዉ�ȋc�_�����Ȃ����߂ɂ́C ���̏͂Ŏ������悤��3�����̒e�Y�����f����p���āC ��K�͂Ȑ��l��͂ɂ���ďI�Nj������m�F���Ă������Ƃ��ł��d�v���낤�B �������C���̏ꍇ�����Ȃ�̍���������C����ɂ��Ă͌�q����B
����ł́C�}-9.60�̗��[�Œ���ɓ����z�d��
�ڂ��Ă���ꍇ���C�����悤�ɍl���Ă݂悤�B
�I�Ǐ�Ԃ�![]() �͎�(9.220)����
�͎�(9.220)����
�Ƃ������x���ł���B
�܂��C���[�̋Ȃ����[�����g�̕��������̂�����傫���̂ŁC
�ŏ��ɗ��[��![]() �ɂȂ�d���x�������߂��
�ɂȂ�d���x�������߂��
�ƂȂ�B�����ł���`�f�ʂ̎�(9.222)��p�����B
���̏ꍇ�ɂ́C
���[�P���x�����̎�(9.219)��![]() �Ɉ�v���Ă��܂��Ă���B
����
�Ɉ�v���Ă��܂��Ă���B
����![]() ��
��![]() ��2�{�����邽�߁C
��2�{�����邽�߁C![]() �ɑ���1.7��
���S����ݒ肵���ꍇ�C
�����
�ɑ���1.7��
���S����ݒ肵���ꍇ�C
�����![]() �ɑ���3.4�̈��S�����m�ۂ������ƂɂȂ��Ă���B
����ɗ��[���S�Y�����[�����g�ɒB�������Ƃɒ����f�ʂ������~������̂́C
�Ȃ����[�����g�����������z�ɂȂ邱�Ƃɒ��ӂ����
�ɑ���3.4�̈��S�����m�ۂ������ƂɂȂ��Ă���B
����ɗ��[���S�Y�����[�����g�ɒB�������Ƃɒ����f�ʂ������~������̂́C
�Ȃ����[�����g�����������z�ɂȂ邱�Ƃɒ��ӂ����
�ƂȂ�B
�f�ʌ�������ؐ����Ȃ��ꍇ�̋������������̂��C�}-9.63��
�E�オ��̋Ȑ��ł���B
���������̏ꍇ���C�����ޗ����Ɛ��Œf�ʌ������̑�����������ꍇ�ɂ́C
�����}��A�̗����̂悤�ɁC![]() �ɒB���Ȃ���������Ȃ��B
���邢��B�̗����̂悤�ɁC���[����
�ɒB���Ȃ���������Ȃ��B
���邢��B�̗����̂悤�ɁC���[����![]() �ɒB���邱�ƂȂ�����
�\��������B
�����C���s�̍|�\���̐v�K���̂悤�ɁC
�ɒB���邱�ƂȂ�����
�\��������B
�����C���s�̍|�\���̐v�K���̂悤�ɁC![]() ��p����
���S�m�ۂ��邱�Ƃ͓K�ł���ƍl���Ă��悳�������B
�|�͂�����x�̐x����ۗL����������̂ŁC�s�[�N�d�̂悤�ȑ��݂�
���҂ł��邩��C�o�ϐ��͂Ƃ������C
���S���ɂ��Ă͌��s�K�����K���ƒf��ł��������B
�������R���N���[�g���̂悤�ȐƐ��ޗ����܂ލ\���̏ꍇ�ɂ́C
��͂����`��͂ɂ��V�~�����[�V�������v���ɕK�v�ɂȂ邱�Ƃ��킩��B
��p����
���S�m�ۂ��邱�Ƃ͓K�ł���ƍl���Ă��悳�������B
�|�͂�����x�̐x����ۗL����������̂ŁC�s�[�N�d�̂悤�ȑ��݂�
���҂ł��邩��C�o�ϐ��͂Ƃ������C
���S���ɂ��Ă͌��s�K�����K���ƒf��ł��������B
�������R���N���[�g���̂悤�ȐƐ��ޗ����܂ލ\���̏ꍇ�ɂ́C
��͂����`��͂ɂ��V�~�����[�V�������v���ɕK�v�ɂȂ邱�Ƃ��킩��B
�������������Ƃ��Ă��C �����܂ł����f���Ɋ�Â����l�I�Ȋm�F�ł����āC100%�̈��S�� �錾�����킯�ł͂Ȃ����Ƃɂ͏\�����ӂ���K�v������B �܂�C�}-9.63��A��B�� �������ʂ����Đ��l��͂Ő��x�ǂ��\���ł��邩�Ƃ�����肪����B ���͂���͂͂Ȃ͂��^��Ȃ̂ł���B �Ⴆ�Ύʐ^-9.61�̒���̂悤�� �S�������܂ł̋����ɑ��C �ǂ̂悤�ȃ��f�����\�z�ł��邩�z�����ė~�����B ���̗����ɂ����ẮC�ޗ�������ɗ��Ă����i�s���j�� ��K�ɗ\���ł��Ȃ��Ƃ����Ȃ��B �����ĕό`���傫���Ȃ�ƁC����i�K���A���̂ł͂Ȃ��Ȃ��̂ł���B ���̗�j��ɂ����ẮC�ޗ����ɔ����I�ȋT���� �������Đ������Ă������߁C���̔����K�����~�������̂悤�ɒ�`���C �܂����̐����̔��W���𗬂ꑥ�̂悤�ɒ�`���Ȃ���Ȃ�Ȃ��B �R���N���[�g�⍻���̂悤�ȃO�`���O�`���ȍޗ��ɑ��� �����������f�����\�z���邱�Ƃ́C�l�Ԃɂ͂قڕs�\���Ǝv���܂��B ���������ŎЉ��Ս\������v�E���݂��Ă��邱�Ƃ��C��X�� �\���Ɋ̂ɖ����Ă����ׂ��ł���B
���āC�������̎����Ɋ�Â��āC����������ɕω�����悤�� �ޗ��������v�����C����curve-fitting�ɂ���č\�z���������I�ȍ\�����́C ���̎��������͈͓̔��ł����K�p�ł��Ȃ��\��������͖̂��炩���B �܂�C�܂�������̃��f���ɂ͉\�Ȍ��蕨���I�E���w�I�Ȕ����I�� ���f����K�ɉ��肵����ŁC�����I�ȍ\�������\�z����K�v������B ���̂悤�ȋ�T�����̌��ׂ̔����Ɛ����ɂ��ẮC ���ۘ_�I�ł͂��邪�������_ �Ƃ������̂��p�����邱�Ƃ�����̂ŁC ��������������Љ�Ă������B �u���ۘ_�I�v�ƋL�����̂́C�}-9.64�ɖ͎��I�� �������悤�ɁC���U�I�ɑ��݂����T������ۂ̌��ׂƂ��� ��舵���̂ł͂Ȃ��C ������l���������ϓI�ȘA���̂Ƃ��ċߎ���������ł���B
�Ⴆ���̐ϔ䗦��![]() �������݂���Ƃ���ƁC���ۂ̍ޗ��i��ނ�
�Ăԁj�̑̐ϔ䗦��
�������݂���Ƃ���ƁC���ۂ̍ޗ��i��ނ�
�Ăԁj�̑̐ϔ䗦��![]() �ɂȂ�B���̕�ނ�Young����
�ɂȂ�B���̕�ނ�Young����![]() ����
����ƁC���̋��݂̕��ϓI��Young��
����
����ƁC���̋��݂̕��ϓI��Young��![]() �́C
�ł��ȒP��Voigt���f���i�P�Ȃ�̐ϕ��ρj�ł́C
��Young������Ȃ̂�
�́C
�ł��ȒP��Voigt���f���i�P�Ȃ�̐ϕ��ρj�ł́C
��Young������Ȃ̂�
�ɂȂ邱�Ƃ͗����ł���Ǝv���B
�����ŁC�u�����v�Ƃ����p�����[�^��![]() �Ƃ��C���ꂪ
�ޗ����ʼn������̃��f���Ŕ������ĕω�����Ƃ����Ƃ��C
���̍ޗ��̋����I��Young����
�Ƃ��C���ꂪ
�ޗ����ʼn������̃��f���Ŕ������ĕω�����Ƃ����Ƃ��C
���̍ޗ��̋����I��Young����
�Ƃ��Ď�舵���̂��C�������������I�ɈӖ��̂��郂�f���Ɗ�����ꂻ�����B
�������C![]() �̔����K�����~�������̂悤�ɂ��ċK�肵�C���̔��W���i�ω���
�@���j�𗬂ꑥ�̂悤�ɋK�肷��K�v������B
���ꂪ�������l�������ł��ȒP�ȗ��_�ł��낤�B
�Ⴆ�ΊE�ʋT���͓]�ʁi�Y���ό`�j�̒~�ς̌��ʂ��낤����C
�����̔��W���͑Y���̗��ꑥ�̂悤�ȗ����ˑ��̑������ɂȂ邾�낤���C
���̑�����driving force�������I�l�@�œK�ɓ�������K�v�����邾�낤�B
�̔����K�����~�������̂悤�ɂ��ċK�肵�C���̔��W���i�ω���
�@���j�𗬂ꑥ�̂悤�ɋK�肷��K�v������B
���ꂪ�������l�������ł��ȒP�ȗ��_�ł��낤�B
�Ⴆ�ΊE�ʋT���͓]�ʁi�Y���ό`�j�̒~�ς̌��ʂ��낤����C
�����̔��W���͑Y���̗��ꑥ�̂悤�ȗ����ˑ��̑������ɂȂ邾�낤���C
���̑�����driving force�������I�l�@�œK�ɓ�������K�v�����邾�낤�B
�����悤�ɋ����I�ȍ~���������l���邱�Ƃ��ł���B
��ނ̏����~�������艞�͂�
![]() �Ƃ���ƁC
�ɂ͍~�����͂͑��݂��Ȃ�����C���ϓI�ȍ~�����͂�
��(9.223)�Ɠ����悤�ɍl�����������C
���̋��݂̋����I��Mises�̍~����
�Ƃ���ƁC
�ɂ͍~�����͂͑��݂��Ȃ�����C���ϓI�ȍ~�����͂�
��(9.223)�Ɠ����悤�ɍl�����������C
���̋��݂̋����I��Mises�̍~����![]() ��
��
�Ƃ������9.40���ƂɂȂ�B
������
![]() �͎�(9.28)�Œ�`����
�������͂ł���C
�͎�(9.28)�Œ�`����
�������͂ł���C![]() �͋̑̐ϔ䗦�ł���B
�Ⴆ�ΗL���v�f�@�Ő��l��͂�����Ƃ��Ă��C�������A���̂�
���f�����ł��C�����ŎZ�肳��鉞�͂���(9.225)�ɑ������C
���l�������~�����l�����邱�Ƃ��ł���B
��������ɂ́C���ǂ�������(driving force)��
�������邩�Ƃ����������g�ݍ��܂�Ă��Ȃ����C
����ɂ��Ă͗Ⴆ��Gurson���f��[28,77]
�Ƃ����̂�����B
���̃��f���̍~������
�͋̑̐ϔ䗦�ł���B
�Ⴆ�ΗL���v�f�@�Ő��l��͂�����Ƃ��Ă��C�������A���̂�
���f�����ł��C�����ŎZ�肳��鉞�͂���(9.225)�ɑ������C
���l�������~�����l�����邱�Ƃ��ł���B
��������ɂ́C���ǂ�������(driving force)��
�������邩�Ƃ����������g�ݍ��܂�Ă��Ȃ����C
����ɂ��Ă͗Ⴆ��Gurson���f��[28,77]
�Ƃ����̂�����B
���̃��f���̍~������
�ƕ\�����B������![]() �͎�(3.38)��
��`�������ω��͂ŁC���̐Ð����ł���B
�͎�(3.38)��
��`�������ω��͂ŁC���̐Ð����ł���B![]() �`
�`![]() ��Tvergaard��
��`�����ޗ��p�����[�^�ŁC����ݒ肵���z�u�̔����I�ȗ̈��
�L���v�f�@�ʼn�͂������ʂ�p���āCGurson���f�������������ۂ�
�������ꂽ���̂ł���BGurson���f���ł͎O�Ƃ�1�ł���B
���ω��͂��܂܂�Ă���̂́C������������������
��������(driving force)��
���������萬�������肷�镨���I�ώ@�ɏ������Ă���B
���̎�(9.226)��
��Tvergaard��
��`�����ޗ��p�����[�^�ŁC����ݒ肵���z�u�̔����I�ȗ̈��
�L���v�f�@�ʼn�͂������ʂ�p���āCGurson���f�������������ۂ�
�������ꂽ���̂ł���BGurson���f���ł͎O�Ƃ�1�ł���B
���ω��͂��܂܂�Ă���̂́C������������������
��������(driving force)��
���������萬�������肷�镨���I�ώ@�ɏ������Ă���B
���̎�(9.226)��![]() (
(![]() )��
)��![]() �Ƃ���C
��(9.225)�ƈ�v����B
�܂莮(9.225)����ʉ��������f���Ȃ̂ł���B
�����ɂ��curve-fitting�ɔ�ׂĐ����ɕ����I�l�@���l������Ă��邱�Ƃ����炩���B
���Ƃ́C����������K����
�������E���̂���
���W�����I�l�@���f��������C
�ό`�Ƌ��Ɋg���鑹�����l�����Ȃ���C�\���̒e�Y�����l��͂��\�ɂȂ�B
��������ł��Ȃ��C�Ǐ��I�ȉ��͏W����T����[�̓��ِ��͍l���ł��Ă��Ȃ��B
�܂������ߒ��ŊE�ʂɐ�����\���̂���͏o�������l������Ă��Ȃ��B
�Ƃ���C
��(9.225)�ƈ�v����B
�܂莮(9.225)����ʉ��������f���Ȃ̂ł���B
�����ɂ��curve-fitting�ɔ�ׂĐ����ɕ����I�l�@���l������Ă��邱�Ƃ����炩���B
���Ƃ́C����������K����
�������E���̂���
���W�����I�l�@���f��������C
�ό`�Ƌ��Ɋg���鑹�����l�����Ȃ���C�\���̒e�Y�����l��͂��\�ɂȂ�B
��������ł��Ȃ��C�Ǐ��I�ȉ��͏W����T����[�̓��ِ��͍l���ł��Ă��Ȃ��B
�܂������ߒ��ŊE�ʂɐ�����\���̂���͏o�������l������Ă��Ȃ��B
����C�|�̏ꍇ�ɂ͂��������������͍l������K�v�������Ǝv����������Ȃ����C ���������I�ɒe�Y���������ώ@����ƁC�������̑傫���Ɉˑ������T���������� ������������\��������B �����ޗ��̂悤�ɐl�דI�Ȕ����\���������ޗ��ł��C ���َ̈�ޗ��E�ʓ��ɋT�������邱�Ƃ� �ώ@����Ă���B�t�^-F�ɏ����� �j��͊w�ɂ��C�T����[�̉��͂̓��ِ��͋T�������̕������� �[���W���Ă��邱�Ƃ��킩���Ă��邩��C �����������T�������܂ލޗ����f���ɂ́C�P�������⍻���q�E�@�ۂ� ���@�̂悤�Ȓ����̕�����9.41�� �܂܂�邱�Ƃ��C������������e�Ղɗ\�z�����B ���̂悤�ȍl�@����C���̂悤�Ȓ������������� �Ə̂��āC�\�����ɓ������邱�Ƃ�����B ������ɂ��Ă��C��Ɏ����̗��ɐ��ޕ����@���邱�Ƃ��ł��d�v�Ȏp���ł���B ������
���̓ǎ҂ɂ́C�ǂ�ǂ�ʔ������_��f�����_�炩���]�̒��� �\�z���Ă��������C�H�w�̔��W�Ɋ�^���ė~�����B