��-2�ł͐Ò�����Љ�C�ό`���Ē�R����ג����\���̒�R�́C ���͂ƋȂ����[�����g�E����f�͂������B �������C�Ō�̗�̂悤�ɎO�ӏ����x�����ꂽ2�a�ԘA�����̏ꍇ�ɂ́C �Ȃ����[�����g�͂��납�x�_���͂��狁�߂邱�Ƃ��ł��Ȃ������B ���̂��ߏ�-3�ł́C �ό`���̂��̂ƒ�R�͂̒�`�ƁC �����p�����ޗ��̒�R�̋L�q�E���f���ɂ��Ċw��ł����B �����ł͂��̒m�����������āC�ǂ�ȗ��ł�������悤�ȗ��_�̒莮��������B
�����_�����ɍג��������C ������ʓI�ɏ����ƁC3������Ԃɉ�����镨�̂̂���1�����ւ� �g�肪����2�����ւ̊g����������Ȃ�傫�Ȃ��̂Ƃ��Ē�`�����B ���̂悤�ȕ��̂ł���C���@����Ԓ��������ւ̗͊w���ʂ̕ω��� ��ׂđ���2�����ւ̕ω��͂���قǑ傫���Ȃ炸�C���炩�̊ȗ��� ���Ȃ킿�ߎ����ł��邩������Ȃ��B ���������������ߎ��ɂ���ē��邱�Ƃ��ł��闝�_�������ŁC���� �������p���肪�������炢�̐��x�������Ƃ��ł���C �ό`�ł��镨�̗̂͊w�Ƃ���2�������邢��3������͂�������C ���Ȃ��Ƃ��v�i�K�ł͂ƂĂ����p�I�ł���B ���̏͂ł́C�����������H�w�I�ɗL�p�ȗ��_�Ƃ��ẮC�Ȃ�����_�� �͊w�̒莮�����s���B�Ȃ�����_���ނ��� �ƌĂ�ł���B ��������b���_���ڏq�������̂ŁC�A�[�`��Ȑ����̂悤�� �Ȃ������_�i�Ȃ�����j�̗͊w�ɂ��Ă� �G��Ȃ��B �܂��g���X�̌��ނ̂悤�Ɏ��͂���_���ނ����ƌĂԁB ���̎������̗͊w�ɂ��Ă͍ŏ��̒莮���ł̂݊܂߁C ��������̗͊w�ɂ��Ă̐߂ł͖�������B �Ȃ��C���̕����ɂ͗͊w���_�̔w�i�Ɗ�{�I�ȉ��p�������L����Ă���̂ŁC ������Đg�ɕt���邽�߂ɂ́C����[106]���� �����̖��������ė~�����B
�Ȃ�������ɍג����_����ƌĂԂ��Ƃɂ������C �ȒP�ȃX�|���W�̎����i�}-4.1�̉E���̎ʐ^�j�� �͂��ߑ����̎�������C�}-4.1�̍����Ɏ������悤�ȁC ���̓�̊�{�I�ȉ����݂��邱�Ƃ��ł������Ȃ��Ƃ��킩���Ă���B
���̊�{�I�ȉ�������Ȃ���Ȃ�����
����Bernoulli-Euler�����邢���������ƌĂсC
���̐߂Œ莮������闝�_�����������_
�ƌĂԂ��Ƃ�����B���ƂŐ}-4.4�ł�
�������邪�C��-3�̍Ō��
���ŋ��߂����̉��͐����̉��̎�(3.131)����
�Ђ��ݐ������v�Z����C
�Ȃ�����ג����_�ŏ�̓�̉��肪�ߎ��I��
�������邱�Ƃ��m���߂邱�Ƃ��ł���B
�����ł͊ȒP�̂��߂ɂ��C�܂������_�̊�b��
�������߂ɂ��C��-2��
��Ƃ��Ĉ������悤��![]() -
-![]() �ʓ��i��-2�ł�
�ʓ��i��-2�ł�![]() -
-![]() �ʓ��j��
�ό`������݂̂�ΏۂƂ���B
�ʓ��j��
�ό`������݂̂�ΏۂƂ���B
�}-4.1�Ɏ������悤��![]() ������̍ג���������
��`���C�����ψʑO������
�ƌĂԂ��Ƃɂ���B�܂��C���d��d�������������ɍ�p���邱�Ƃ�C
��q�̋Ȃ����[�����g�̐��̌�����O���ɒu���āC
������̍ג���������
��`���C�����ψʑO������
�ƌĂԂ��Ƃɂ���B�܂��C���d��d�������������ɍ�p���邱�Ƃ�C
��q�̋Ȃ����[�����g�̐��̌�����O���ɒu���āC![]() ����������������
��`���C
����������������
��`���C![]() -
-![]() �ʓ��̋Ȃ��ό`�����̏͂ł͑ΏۂƂ���B
�������f��������ɓ������Ă̓�̉������-3��
�������Ђ��݂ŕ\���ƁC��1�̉����
�ʓ��̋Ȃ��ό`�����̏͂ł͑ΏۂƂ���B
�������f��������ɓ������Ă̓�̉������-3��
�������Ђ��݂ŕ\���ƁC��1�̉����
�ł���B�܂�C�f�ʌ`�ω����Ȃ����Ƃ�![]() -
-![]() �ʓ���2������
�L�тƊp�ω�����ɂȂ邱�Ƃł���B�܂���2�̉����
�ʓ���2������
�L�тƊp�ω�����ɂȂ邱�Ƃł���B�܂���2�̉����
(4.2)
�ƂȂ�B�܂�C�����ł͈�ʘ_�Ƃ���![]() -
-![]() ,
, ![]() -
-![]() �ʂ̗�����
���グ�Ă݂����C�Ȃ�����ʓ��ł̊p�ω�������
������Bernoulli-Euler�̉���ł���B
�ʂ̗�����
���グ�Ă݂����C�Ȃ�����ʓ��ł̊p�ω�������
������Bernoulli-Euler�̉���ł���B
�}-4.2��
�������悤�ɗ��̍ג���������![]() �����Ɉ�v������ƁC���
�Ђ��ݏ�̉��莮(4.1) (4.2)��
���}�̂悤�Ȃ����Ԃ�`�����ƂɂȂ�B
���Ȃ킿�f�ʌ`�s�ς̉���ɂ��C
����f�ʂ�
�����Ɉ�v������ƁC���
�Ђ��ݏ�̉��莮(4.1) (4.2)��
���}�̂悤�Ȃ����Ԃ�`�����ƂɂȂ�B
���Ȃ킿�f�ʌ`�s�ς̉���ɂ��C
����f�ʂ�![]() ������
������![]() �������ꂽ�_A�́C
������Ƃ������Ԃ̎����i�j���j���瓯�������������ꂽ�_B��
�ψʂ���B�܂�Bernoulli-Euler�̉���ɂ��C
�������ꂽ�_A�́C
������Ƃ������Ԃ̎����i�j���j���瓯�������������ꂽ�_B��
�ψʂ���B�܂�Bernoulli-Euler�̉���ɂ��C![]() ����
�������Ă����C�ӂ̒f�ʂ͂�����Ƃ������ƒ�������B
���������āC�_A��2�����̕ψʐ����͊w�I�ȊW����
����
�������Ă����C�ӂ̒f�ʂ͂�����Ƃ������ƒ�������B
���������āC�_A��2�����̕ψʐ����͊w�I�ȊW����
�ƂȂ邱�Ƃ����炩�ł���B![]() ��
�f�ʂ��������ψ��C
��
�f�ʂ��������ψ��C![]() ��������C
�����
��������C
�����![]() ������݊p
�ƌĂԁB�㎮�̍Ō�̕\���ł͂���݊p
������݊p
�ƌĂԁB�㎮�̍Ō�̕\���ł͂���݊p![]() �����ɏ������͈͂�
���_�ł���Ƃ��C
�����ɏ������͈͂�
���_�ł���Ƃ��C![]() �̏���
��
�̏���
��
![]() ,
,
![]() �Ƌߎ����C����݊p��2�����ȏ�����Ă���B
�Ƌߎ����C����݊p��2�����ȏ�����Ă���B
����Bernoulli-Euler�̉��莮(4.2b)�ɂ��̐������������
�ƂȂ�C����݊p������݂̈�K�̔��W���ŕ\���ł��邱�Ƃ�
�����Ă����B�܂�
�ł���B���̕����ł͂���݊p���v���𐳂Ƃ��Ē�`�������߁C �E�ӂɃ}�C�i�X�L��������B ���̂悤�ɁC�����ȕψʂ��������Ȃ��͈͂ł̗��̕ψʐ�����
(4.5)
�ƂȂ�B
��Ȃ��Ƃ́C�C�ӓ_�̕ψʂ�������̓_�̕ψʁi![]() ������
���j
������
���j![]() ��
��![]() ��
��![]() ��1���������ŕ\���ł��Ă��邱�Ƃł���B
��1���������ŕ\���ł��Ă��邱�Ƃł���B
�O�߂̉�����C��łȂ��Ђ��ݐ�����
���̏ꍇ�ɂ�![]() �����ɂȂ�B
��`�ɏ]���āC��(4.5a)����(3.6)�ɑ�������
�����ɂȂ�B
��`�ɏ]���āC��(4.5a)����(3.6)�ɑ�������
�ƂȂ�B
�܂�����Ȃ����ꍇ�ɔ�������Ђ��݂́C�}-4.3��
�������悤��
![]() �̔C�ӂ̒f�ʂ�
�̔C�ӂ̒f�ʂ�![]() ������
���`���z�����邱�Ƃ��킩��B�������Ђ��݂̎O�p�`���z
�ƌĂ����̂ł���B
������
���`���z�����邱�Ƃ��킩��B�������Ђ��݂̎O�p�`���z
�ƌĂ����̂ł���B
![]() �͎����̐L��
�ł���C
�͎����̐L��
�ł���C
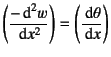 ��
�ό`���ċȂ��������̎����̋ȗ�
��\������B
��(4.6)���C���̒f�ʓ��̔C�ӓ_�̂Ђ��݂��������
��̗ʂ�
��
�ό`���ċȂ��������̎����̋ȗ�
��\������B
��(4.6)���C���̒f�ʓ��̔C�ӓ_�̂Ђ��݂��������
��̗ʂ�![]() ��1����������
�\�����Ƃ��ł��邱�Ƃ������Ă���B���̂����肪�\���͊w�̓����ł���B
�܂�C���m����
��1����������
�\�����Ƃ��ł��邱�Ƃ������Ă���B���̂����肪�\���͊w�̓����ł���B
�܂�C���m����![]() �����̊��ɂȂ�̂ŁC�O�̘͂A���̗̂͊w�Ƃ͈قȂ�C
�ŏI�I�Ȏx�z��������������������ɂȂ�B
�����̊��ɂȂ�̂ŁC�O�̘͂A���̗̂͊w�Ƃ͈قȂ�C
�ŏI�I�Ȏx�z��������������������ɂȂ�B
�����ł͒e�������_��莮���������̂ŁC
��(4.6)��1������Hooke�̖@���C�܂�
��(3.116a)�ɑ������C�����͂�
�ƂȂ�B![]() ��Young���ł���B
�Ђ��݂��}-4.3�̂悤�ɐ��`���z���Ă��邩��C
���͂����l�ɐ��`���z������B����͏�-3��
��(3.131a)�̉E�ӑ�1���ɑ������Ă���B
���̎����C�ޗ��̒�R����\���\�����ł���C���̊W����
�s�Ò�\���̉�͂ɂ͕K�v�ɂȂ�̂ł���B
�܂�C���ۂɂǂ��������ό`�������C���̍ޗ����ǂ̂悤�Ȓ�R�͂�
�������Ēf�ʗ͂�������̂��Ƃ��������C
���̎�(4.7)���^���Ă����B
����ɂ���āC2�a�ԘA�����̂悤�ȕs�Ò�\����������悤�ɂȂ�B
��Young���ł���B
�Ђ��݂��}-4.3�̂悤�ɐ��`���z���Ă��邩��C
���͂����l�ɐ��`���z������B����͏�-3��
��(3.131a)�̉E�ӑ�1���ɑ������Ă���B
���̎����C�ޗ��̒�R����\���\�����ł���C���̊W����
�s�Ò�\���̉�͂ɂ͕K�v�ɂȂ�̂ł���B
�܂�C���ۂɂǂ��������ό`�������C���̍ޗ����ǂ̂悤�Ȓ�R�͂�
�������Ēf�ʗ͂�������̂��Ƃ��������C
���̎�(4.7)���^���Ă����B
����ɂ���āC2�a�ԘA�����̂悤�ȕs�Ò�\����������悤�ɂȂ�B
���Ĉ���C��(4.2b)�����̂܂܂���f��Hooke�̖@��
��(3.114b)��
�������ƁC����f���͂͒f�ʂɂ͔������Ă��Ȃ����ƂɂȂ�B
���̂���f���͂ɂ��Ă̌��_�͑f���ɂ͎�����Ȃ��Ǝv����B
�Ƃ����̂��C
���̂Ђ��ݕ��z��M����Ȃ�C���͔��ɔ������������d�˂�
���̂Ƃ��ă��f�����ł��C���ꂼ��̔����݂��ɂ��ׂ��
�����d�Ȃ������������C�������C����f��R�͖����܂�
�P�ɐL�яk�݂̕ό`�݂̂ɂ���Ē�R���Ă��邱�ƂɂȂ�B
�܂�����͎�(3.131b)�ɔ�����B
�������ג������̂ł́C![]() �̑傫���ɔ�ׂĔ�r�I
����������f����
�̑傫���ɔ�ׂĔ�r�I
����������f����![]() �����������Ȃ����Ƃ́C
�������(3.131)���玦�����Ƃ�
�ł���B�}-4.4��
��(3.131)����Z�肳��鉞�͂̍ő�l���m�̔���ׂ�
���̂ŁC
�����������Ȃ����Ƃ́C
�������(3.131)���玦�����Ƃ�
�ł���B�}-4.4��
��(3.131)����Z�肳��鉞�͂̍ő�l���m�̔���ׂ�
���̂ŁC
![]() ,
,
![]() ,
,
![]() ��
��`���āC���ꂼ��̔���ג���
��
��`���āC���ꂼ��̔���ג���
![]() �ɑ��Ď��������̂ł���B
���̂悤�ɍג������ł́C
�ɑ��Ď��������̂ł���B
���̂悤�ɍג������ł́C![]() �ɔ�ׂđ���2�������ꌅ���炢��������
�ɔ�ׂđ���2�������ꌅ���炢��������
| (4.8) |
�ł��邱�Ƃ��킩��B�܂�C��(4.7)�œ���
���͓͂�̊�{�I�ȉ���������ɗp�������Ƃɂ�錋�_�ł��邪�C
���̉��肻�̂��̂͐}-4.4���x��
�덷���邢�͋ߎ��x�������Ă���Ƃ������Ƃɂ�
���ӂ���K�v������B
�܂�C���������_���ג������̂ɑ����ߎ����ɉ߂��Ȃ����Ƃ�
���炩�ł���B
�������̗��_��p�������C�������Ƃ̔�r����C
���Ɏ�(4.7)�̒�����![]() ��
�H�w�I�ɏ\���Ȑ��x�Ōv�Z�ł��邱�Ƃ��킩���Ă���B
���������đ�_�ł͂��邪�K�ȉ���Ō��ۂ����f�������邱�Ƃɂ��C
������������ŕ\������Ď�舵�����y�ȗ��_�������ɍ\�z����悤��
������B
���������ߎ��x�̍�������f���̗͂U���ɂ��Ă͌�q����B
��
�H�w�I�ɏ\���Ȑ��x�Ōv�Z�ł��邱�Ƃ��킩���Ă���B
���������đ�_�ł͂��邪�K�ȉ���Ō��ۂ����f�������邱�Ƃɂ��C
������������ŕ\������Ď�舵�����y�ȗ��_�������ɍ\�z����悤��
������B
���������ߎ��x�̍�������f���̗͂U���ɂ��Ă͌�q����B
��-2�ŗU���������̒�R�͂܂�f�ʂɔ�������
�f�ʗ́i�����́j���C�Ђ��݂��邢�͕ψʂƂǂ̂悤�ȊW��
�L���Ă��邩�ɂ��ẮC
��̌��ʂ��e�����͂̒�`�ɑ������킩��B�܂��C����
�͒f�ʓ��̒����͂̑��a�ł��邩��
�ƂȂ�B������
| (4.10) |
�Œ�`����C![]() ���f�ʐ��C
���f�ʐ��C![]() ���f��1��
���[�����g
�ƌĂ��f�ʒ萔�ŁC�����ɒf�ʂ̌`��݂̂Ɉˑ������萔�ł���B
���f��1��
���[�����g
�ƌĂ��f�ʒ萔�ŁC�����ɒf�ʂ̌`��݂̂Ɉˑ������萔�ł���B
����C�Ȃ����[�����g
��![]() �����̋��͂ɂ���R�͂ł��邩��
�����̋��͂ɂ���R�͂ł��邩��
�Ƃ����W�ɂȂ�B������![]() ���f��2�����[�����g
�ƌĂ��f�ʒ萔4.1��
���f��2�����[�����g
�ƌĂ��f�ʒ萔4.1��
| (4.12) |
�Œ�`�����B ���̓�̊W��(4.9) (4.11)���C �f�ʗ͂Ǝ����̕ψʂ̊Ԃ̊W���Ƃ��ĕ\�������L�`�̍\����4.2�ł���C �s�Ò�\���������̂ɕK�v�ȊW���Ȃ̂ł���B
�Ȃ��O�߂ł��q�ׂ��悤�ɁC����ɂ���Ă���f�Ђ��݂��� ���Ă��邽�߁C���̉���͈̔͂ł͂���f���͂���ɂȂ邩��C �f�ʗ͂Ƃ��Ċm���ɑ��݂���͂��̂���f�͂́C��̂悤�� �ό`�ƊW�t������ʂƂ��Ă͒�`�ł��Ȃ��B ����͔�r�I�ȒP�ȋ��E�l���Œ����͂x�ǂ����߂邽�߂� �莮�����ꂽ���������_���������_�ł���B ���������Ă��̐߂ł́C�ψʂ�ό`�ƒ��ڊW�t����ꂽ�f�ʗ͂Ƃ��Ă� ����f�͂͒�`���邱�Ƃ͂ł��Ȃ����C ���߈ȍ~�ł͂������l������B���������������V����I�� ����f�͂̓��������C�ɏ����Ȃ��ꍇ�ɂ́C�t�^-C�Ɏ����� ���z�d���ɂ��x�z�������̗U�����Q�Ƃ��ė~�����B
����![]() �����f�ʂ��}�S
��ʂ�悤�ɐݒ肳��Ă���C
�}�S�̒�`���u���̓_�����_�Ƃ����f��1�����[�����g�����
�Ȃ�_�v�ł��邱�Ƃ���
�����f�ʂ��}�S
��ʂ�悤�ɐݒ肳��Ă���C
�}�S�̒�`���u���̓_�����_�Ƃ����f��1�����[�����g�����
�Ȃ�_�v�ł��邱�Ƃ���
�ƂȂ�C��̓�̒f�ʗ͂ƕψʐ����̊W�͕����ł�
(4.13)
�ƕ\�����Ƃ��ł���B��(4.13b)�ł͎�(4.4)�̊W��
�p���Ă���B�܂�C���͂��L�э���![]() ��
��R�W���Ƃ������̐L��
��
��R�W���Ƃ������̐L��
![]() �Ƃ���
�ό`�ɂ���R�͂ł���̂ɑ��C�Ȃ����[�����g�͎�����
�ȗ�
�Ƃ���
�ό`�ɂ���R�͂ł���̂ɑ��C�Ȃ����[�����g�͎�����
�ȗ�
![]() �Ƃ���
�ό`�ɂ���R�͂ł��̒�R�W�����Ȃ�����
�Ƃ���
�ό`�ɂ���R�͂ł��̒�R�W�����Ȃ�����![]() ��
���邱�Ƃ������Ă���B����������
�����f�ʐς����f�ʓ��m�Ŕ�r�����Ƃ��C
���[���f�ʂ̂悤�ɒf��2�����[�����g���傫���Ȃ�`�̕���
���傫�ȋȂ���R�͂�L���闝�R�������ɂ���B
��
���邱�Ƃ������Ă���B����������
�����f�ʐς����f�ʓ��m�Ŕ�r�����Ƃ��C
���[���f�ʂ̂悤�ɒf��2�����[�����g���傫���Ȃ�`�̕���
���傫�ȋȂ���R�͂�L���闝�R�������ɂ���B
���āC�����͂ƂЂ��݂���ђ����͂Ƃ̊W�����߂邽�߂� ��(4.6) (4.7)�� ��(4.13)��������ƁC�L�тЂ��݂ƒ����͂�
(4.14)
�ƕ\���ł���B���̂悤�ɁC
�Ȃ����镔�ނɐ����鉞�͂͒f�ʂ̏㉺���ōő�ɂȂ邽�߁C
�Ⴆ�C����������ł����ꂽ�f�ʂ̉��܂ł�![]() ����
���W�l���C
����
���W�l���C![]() �̕������i����j��
�̕������i����j��
![]() �C
�������i�����j��
�C
�������i�����j��![]() ��
�\�����Ƃɂ���ƁC���̒f��
��
�\�����Ƃɂ���ƁC���̒f��![]() �ł�
�����̍ő剞�́i�ŊO������
�ł�
�����̍ő剞�́i�ŊO������
![]() ,
,
![]() �j��
�j��
�ƂȂ�B������
�Œ�`������f�ʌW��
��p����ƁC�Ȃ�![]() �Ǝ���
�Ǝ���![]() ������ɔ�������i�����́j�ő剞�͂�
������ɔ�������i�����́j�ő剞�͂�
�ƕ\�����Ƃ��ł���B
�����ł̒�`�ł�![]() �͕����������߁C�����W�̒�`�Ƃ�
�قȂ�i��Βl�͓����j���Ƃɒ��ӂ��ė~�����B
�͕����������߁C�����W�̒�`�Ƃ�
�قȂ�i��Βl�͓����j���Ƃɒ��ӂ��ė~�����B
![[*]](../crossref.gif) �̖ї����A�̈�b�Ɋ֘A���Ď�����3�{�̖��
�g�f�ʂ̒������ƒf��2�����[�����g�ƒf�ʌW�������߂�B
�̖ї����A�̈�b�Ɋ֘A���Ď�����3�{�̖��
�g�f�ʂ̒������ƒf��2�����[�����g�ƒf�ʌW�������߂�B

�ŎZ��ł��邱�Ƃ������B����ɁC�|�̔\���̂悤�ɓ�����
���ɔ����ꍇ
![]() �ɂ́C�㎮�E�ӂ̑�1����
���������ȕւȕ\���ŋߎ��ł��邱�Ƃ��m�F����B
�ɂ́C�㎮�E�ӂ̑�1����
���������ȕւȕ\���ŋߎ��ł��邱�Ƃ��m�F����B
�����ŗU������荇�����͗��̒��̂���_![]() ��
�ߖT�ɂ�����Ǐ��I�Ȃ荇������
����C��-2�̑O���őΏۂƂ��Ă����O�͂Ǝx�_���͂�
�荇���̂悤�ȗ��S�̂̋����I�Ȃ��̂Ƃ͈قȂ�B
�܂��-2.3.5�ŗU������
�����������ŕ\�����荇�������C������x�C
���̂���������v�f
��
�ߖT�ɂ�����Ǐ��I�Ȃ荇������
����C��-2�̑O���őΏۂƂ��Ă����O�͂Ǝx�_���͂�
�荇���̂悤�ȗ��S�̂̋����I�Ȃ��̂Ƃ͈قȂ�B
�܂��-2.3.5�ŗU������
�����������ŕ\�����荇�������C������x�C
���̂���������v�f![]() �����o���āC���͂��܂߂�
�����ɐ����Ă�����́i�f�ʗ́j�ƕ��z�O�͂̂荇����������
���߂悤�Ƃ��Ă���B
�����o���āC���͂��܂߂�
�����ɐ����Ă�����́i�f�ʗ́j�ƕ��z�O�͂̂荇����������
���߂悤�Ƃ��Ă���B
�}-4.6�̂悤�ɕ��z�O�͂���p���C�O�߂�
�q�ׂ��悤�ɍ����͂Ƃ��Ă̂���f�͂��������Ă���Ƃ���ƁC
���̔������v�f��![]() �����̗͂̂荇����
�����̗͂̂荇����
�ƂȂ邱�Ƃ���
������f�͂̂荇���ł���B
���ɓ_A�̔����v���̃��[�����g�̂荇�����Ƃ��Ă݂��
�ƂȂ邪�C���z�O�͂ɂ�鍀��2���̔������ƂȂ邽�߁C����
�����[�����g�̂荇���ɂȂ�B���̎���
�t��
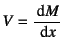 �ƌ��āC
����f�͂��Ȃ����[�����g�̕ω����Œ�`����Ă����
�l���Ă������x���Ȃ��B
�ƌ��āC
����f�͂��Ȃ����[�����g�̕ω����Œ�`����Ă����
�l���Ă������x���Ȃ��B
��(4.18)����(4.17)�ɑ�����邱�Ƃ�
����Ă킯�̂킩��Ȃ�����f�͂���������������Ă��܂��ƁC
�Ȃ��Ɋւ���荇����
��
�ł������Ƃ��킩��B
�Ō��![]() �����̗͂̂荇������C���͂̂荇����
��
�����̗͂̂荇������C���͂̂荇����
��
�Ƌ��߂���B
�O�߂ŋ��߂��荇�����́C����![]() �̗��Ȃ�
�̗��Ȃ�![]() ��
�C�ӓ_�Ő������Ȃ���Ȃ�Ȃ��B����ɕ��z�O�͈ȊO�̊O�͏�����x��������
�l������ɂ́C���E�����i�A�������j�Ƃ������̂�^���Ă��K�v������B
�����ł͊ȒP�̂��߂ɁC����
��
�C�ӓ_�Ő������Ȃ���Ȃ�Ȃ��B����ɕ��z�O�͈ȊO�̊O�͏�����x��������
�l������ɂ́C���E�����i�A�������j�Ƃ������̂�^���Ă��K�v������B
�����ł͊ȒP�̂��߂ɁC����![]() ��1�{�̗������[��
�x������Ă���悤�ȏꍇ��ΏۂƂ��C���̒[���ł̏����Ƃ��Ă�
���E������U���������B
��1�{�̗������[��
�x������Ă���悤�ȏꍇ��ΏۂƂ��C���̒[���ł̏����Ƃ��Ă�
���E������U���������B
��{�I�ɋ��E�����ɂ�2��ނ���B��͕ψʂ�^�������
�ł���B���Ȃ킿���̏ꍇ�ɂ́C���̗^����ψʐ����Ƃ���![]() ������
�����ړ��ʂ�
������
�����ړ��ʂ�![]() ������
����݂��l�����邪�C���͂��������B
����͏�-2�ŗ�Ƃ��ĉ������Ў������̕Ǒ���
�������l���Ă݂�Ζ��炩�ł��邪�C�܂�C����݂����ł�
�Ȃ�����݊p
������
����݂��l�����邪�C���͂��������B
����͏�-2�ŗ�Ƃ��ĉ������Ў������̕Ǒ���
�������l���Ă݂�Ζ��炩�ł��邪�C�܂�C����݂����ł�
�Ȃ�����݊p![]() ����ɂȂ鋫�E�����߂��ݒ[�ł���B
�ȏ�̊w�I�ȍl�@����C
����ɂȂ鋫�E�����߂��ݒ[�ł���B
�ȏ�̊w�I�ȍl�@����C![]() ,
, ![]() ��
��![]() ����
����
����
����
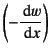 ��
�^����̂��ψʂ̋��E����
�ŁC�w�I���E����
�Ƃ��Ă�4.3��B
��
�^����̂��ψʂ̋��E����
�ŁC�w�I���E����
�Ƃ��Ă�4.3��B
������̏����͊O�͂���p���Ă��鋫�E�ł̂��̂� ����B��-3�Œ�`�����悤�ɁC ���͔͂������Ă���ʂ̊O�����@�����������ɂȂ�悤�� ��`����Ă��邽�߁C���͂̒f�ʓ��̍��v�Ƃ��čl���Ă���f�ʗ͂��C �f�ʂ̖@�������W�̂ǂ���̕����������Ă��邩�ɂ���Ă��̕������قȂ�B ����ɑ��C�O�͂̐����̐��̌����͏�ɍ��W�̐��̕����Œ�`����̂� ���ʂł���B�Ȃ��ɂ��Ă͊��ɐ�-2.3.5�� �����������C�ēx�C���̋��E�����ɂ��Ă͐}��p���Ē��Ӑ[���U�����邱�Ƃ� ���悤�B
�}-4.7�Ɏ������̂�![]() �܂���W�l��
���������̒[�ł̏����ł���B���̒[���̌����̖���������
��o���ƁC���̗��������̖ʂ�
�܂���W�l��
���������̒[�ł̏����ł���B���̒[���̌����̖���������
��o���ƁC���̗��������̖ʂ�![]() ���̐�������@���x�N�g����
���鐳�̖ʂł��邩��C�f�ʗ͂����W�̐��̕��������ׂĐ���
���͂ł���B����C�O�͂͐}�̂悤�ɍ��W���������ׂĐ��̌�����
���Ē�`�����B���̌����̖��������̗͂̂荇�����
���̐�������@���x�N�g����
���鐳�̖ʂł��邩��C�f�ʗ͂����W�̐��̕��������ׂĐ���
���͂ł���B����C�O�͂͐}�̂悤�ɍ��W���������ׂĐ��̌�����
���Ē�`�����B���̌����̖��������̗͂̂荇�����
�ƂȂ�Ȃ���Ȃ�Ȃ�����C���[�ł��͂̋��E����
�͎��̂悤�ɂȂ�B
����}-4.8��![]() ���C�܂���W�l��
�傫���[�ł̏����ł���B���̏ꍇ�C���͂̍�p����ʂ�����
�ʂł��邱�Ƃɒ��ӂ���C�E�[�ł̗͂̋��E������
���C�܂���W�l��
�傫���[�ł̏����ł���B���̏ꍇ�C���͂̍�p����ʂ�����
�ʂł��邱�Ƃɒ��ӂ���C�E�[�ł̗͂̋��E������
�ƂȂ邱�Ƃ͖��炩�ł���B�͂̋��E�������͊w�I���E���� �Ƃ��Ă��4.4���C ����͒[���̒f�ʂ����̖ʂȂ̂����̖ʂȂ̂��Ŕ����ɕ������قȂ��� ���邱�Ƃɒ��ӂ��ׂ��ł���B
�ȏ��2��ނ̋��E���������ꂼ��̒[���ł��ꂼ��Z����
���邪�C���̔C�ӂ̑g�ݍ��킹�C���邢�͂��ׂĂ�^���邱�Ƃ�
�ł��邾�낤���B���̓����͔ۂł���C������
�g�ݍ��킹�ŋ��E������^���Ȃ���������B��ɒ�܂邱�Ƃ�
�����B�Ⴆ�Ύx����͂���݂��ɂ�����������C������
���̔��́i���̏ꍇ��![]() �����O�́j�����^�����邾�낤���B
�Ò�\���łȂ����肱�̎x�_���͂�\�ߗ^���邱�Ƃ͂ł��Ȃ����߁C
��ʘ_�Ƃ��ė������ɗ^���邱�Ƃ͂ł��Ȃ����Ƃ��z���ł���B
���̂悤�ɍl���Ă���ƁC�������g�ݍ��킹�̋��E����
��
�����O�́j�����^�����邾�낤���B
�Ò�\���łȂ����肱�̎x�_���͂�\�ߗ^���邱�Ƃ͂ł��Ȃ����߁C
��ʘ_�Ƃ��ė������ɗ^���邱�Ƃ͂ł��Ȃ����Ƃ��z���ł���B
���̂悤�ɍl���Ă���ƁC�������g�ݍ��킹�̋��E����
��
![]() �ł���C
���ꂼ��̒[���œK�ɎO���^�����Ȃ���Ȃ�Ȃ����Ƃ�
���炩�ɂȂ�B�㎮�ł͊ȒP�̂��߂�
�ł���C
���ꂼ��̒[���œK�ɎO���^�����Ȃ���Ȃ�Ȃ����Ƃ�
���炩�ɂȂ�B�㎮�ł͊ȒP�̂��߂�
�Ƃ����L����p�����B
![]() �͒[���f�ʂ̊O�����P�ʖ@��
�x�N�g����
�͒[���f�ʂ̊O�����P�ʖ@��
�x�N�g����![]() �̐������̒P�ʃx�N�g���Ƃ̓��ς̒l�ƍl��������B
���̎�(4.23)�́u���邢�́v�ł͂��ψʂƗ͂̑g�ɂ��ẮC
�d���Ƃ����ϓ_���璭�߂����قǕs�v�c�Ȃ��̂ł͂Ȃ����Ƃ�
�킩��Ǝv���B
�Ⴆ�Ώ�-5�̎�(5.13) (5.19)�̒��Ɨ���
���z�d�����̊O�͍������ė~�����B
�̐������̒P�ʃx�N�g���Ƃ̓��ς̒l�ƍl��������B
���̎�(4.23)�́u���邢�́v�ł͂��ψʂƗ͂̑g�ɂ��ẮC
�d���Ƃ����ϓ_���璭�߂����قǕs�v�c�Ȃ��̂ł͂Ȃ����Ƃ�
�킩��Ǝv���B
�Ⴆ�Ώ�-5�̎�(5.13) (5.19)�̒��Ɨ���
���z�d�����̊O�͍������ė~�����B
�ȏオ��{�I�ȋ��E�����ł��邪�C���̂ɍڂ���ꂽ����e���I��
�x���������̏ꍇ�ɂ́C���̊w�I���E�����Ɨ͊w�I���E������
�������ꂸ�C����g�ݍ��킳��ė^������ꍇ������B
�Ⴆ�ΐ}-4.9�i�}�͉E�[�̏ꍇ�̗�j�̂悤�ɁC
�o�l�W��![]() �̐��`�o�l�Ŏx�����ꂽ�����́C�[���̗͂̂荇������
�̐��`�o�l�Ŏx�����ꂽ�����́C�[���̗͂̂荇������
�ƂȂ邱�Ƃ��킩��B���̋��E�������C��{�I��2��ނ̋��E������ �g�ݍ��킳���������ł��邱�Ƃ���C��3��̋��E���� �ƌĂ�4.5���Ƃ�����B
�ό`�ł�����Ƃ��Ă̎x�z�������Ƌ��E������
���߂�ꂽ���C�\���͊w�̖��͂��̎x�z�����������E�l���
�Ƃ��ĕ\���ĉ������Ƃł���B
�O�߂̂荇�����͓��R�Ò�n�̂��̂Ɠ����ł��邪�C
�����ł͕s�Ò�\�����������Ƃ�O����
�u���C�ȏ�̎x�z�������̂��ׂĂ�ψʐ���![]() ,
, ![]() �ŕ\���Ă��܂����B
�������邱�Ƃɂ���āC��-2�̍Ō�̗�ŏq�ׂ��悤�ȁC
�ό`���܂߂��w�I�Ȑ��������l�����Ȃ���荇������������悤�ɂȂ�B
�����Ŏ�(4.19) (4.20)�̂荇������
��(4.9) (4.11)��������ƁC
���ꂼ��
�ŕ\���Ă��܂����B
�������邱�Ƃɂ���āC��-2�̍Ō�̗�ŏq�ׂ��悤�ȁC
�ό`���܂߂��w�I�Ȑ��������l�����Ȃ���荇������������悤�ɂȂ�B
�����Ŏ�(4.19) (4.20)�̂荇������
��(4.9) (4.11)��������ƁC
���ꂼ��![]() ������
������![]() �����̂荇������
�����̂荇������
![\begin{manyeqns}
&&\D*{}{x} \left\{EA\D*{u(x)}{x}-EJ_z\D*[2]{w(x)}{x}\right\}+p(...
...[2]{}{x} \left\{EJ_z\D*{u(x)}{x}-EI\D*[2]{w(x)}{x}\right\}+q(x)=0
\end{manyeqns}](s1img1173.gif)
(4.26)
�ƕψʐ����ŕ\���ł���B
�������C�����f�ʂ���l�ł���![]() �����}�S��ʂ�悤��
�ݒ肳���C���̓�̎���
�����}�S��ʂ�悤��
�ݒ肳���C���̓�̎���
(4.27)
�Ə������Ƃ��ł���B
�ȉ��C��l�f�ʂ�![]() ���͐}�S��ʂ���̂Ƃ��ċL�q���܂Ƃ߂�B
���͐}�S��ʂ���̂Ƃ��ċL�q���܂Ƃ߂�B
���ɋ��E��������(4.23)��
��(4.9) (4.11)�������C
��(4.18)�̂���f�͂ƋȂ����[�����g�̊W��p���C
����ɐ}�S��ʂ�悤��![]() ����I���Ƃ��l������ƁC
���[
����I���Ƃ��l������ƁC
���[![]() �ɑ���
�ɑ���
�ƂȂ�B
�܂��C��(4.25)�̂悤�Ɋw�I�Ȃ��̂Ɨ͊w�I��
���̂����݂��鋫�E�����̏ꍇ�����l�ȉ��Z�ŕψʕ\���ł��邪�C
���̗�̏ꍇ�ɂ͂���f�͂Ɋւ��鋫�E������
�ɂȂ邾���ł���B ��(4.27)�̂悤�Ɏ��̐L�яk�݂ƋȂ������� �\���ł��邱�Ƃ���C�ʏ�C���̐L�яk�݂Ŏ�ɒ�R���� ���ނ����C��� �Ȃ��Ƃ���f�Œ�R���镔�ނ��� �Ə̂��邱�Ƃ������B�����ė�����g�ݍ��킹���\�������g 4.6�ƌĂԁB�ȉ��ł͗�������ΏۂƂ���B ���i�܂�g���X�j�ɂ��Ă�[124]�Ɍ����ȉ��������̂� �Q�Ƃ��ė~�����B �������C���ۂ̍��g���ނ͒ʏ헧�̓I�ɔz�u����Ă��邱�Ƃ���C �˂�����܂ދȂ������͂��A�������\�����ނɂȂ��Ă��邱�Ƃɂ� ���ӂ���K�v������B ����ɂ��Ă͏�-9�̗��̍��g�̐߂Ő�������B
�ŏ���
���͓����z�O�͂��鍶�[�Œ�E�[�P���x����
�s�Ò���i4.10�j�ł���B
�x�_���͂����œ�C�E�ň�C���v3�Ȃ̂ŁC
�͂̂荇�������ł͉����Ȃ��s�Ò�\���ł��邱�Ƃ͂킩��Ǝv���B
���E������
�ŗ^������B![]() ��
��![]() �Ɋւ�����W����\���Ă���C�ȉ��p�ɂɗp����B
�Ɋւ�����W����\���Ă���C�ȉ��p�ɂɗp����B
�Ō�̋��E�����́C�E�[�͉�]���R�ŁC���̑���O�̓��[�����g��
��p���Ă��Ȃ��Ƃ������̂ł���B
��(4.27b)��![]() ���萔
���萔![]() ��
���邩�������
��
���邩�������
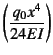 �ƂȂ�B
�ƂȂ�B![]() �������ꍇ��
�i�Ď����邢�͓����j��(4.27b)��
�������ꍇ��
�i�Ď����邢�͓����j��(4.27b)��
![]() ��
������ē��邱�Ƃ��ł�������������̍���
��
������ē��邱�Ƃ��ł�������������̍���![]() ��4�d���ɂȂ�̂ŁC
���̐Ď�����
��4�d���ɂȂ�̂ŁC
���̐Ď�����![]() ��3���������ł���B���������Ĉ�ʉ���
��3���������ł���B���������Ĉ�ʉ���
�ƕ\�����Ƃ��ł���B���W�����Z�肵�Ă�����
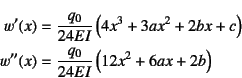
�ł���B �������̋��E�����ɑ�������
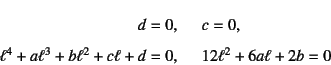
��B���������āC��1�s�ڂ�![]() �ł̌��ʂ��2�s�ڂ�
������Đ�������ƁC
�ł̌��ʂ��2�s�ڂ�
������Đ�������ƁC![]() ��
��![]() �𖢒m���Ƃ����������
�𖢒m���Ƃ����������
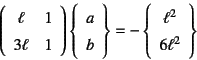
�ƂȂ�̂ŁC�����������![]() ,
, ![]() ��
��
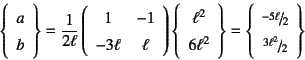
�Ƌ��߂���B���̌��ʂ���(4.30)�ɑ���������C
�C�ӓ_�̕ψʂ�
�ƂȂ�B
�㎮��2���������Ȃ����[�����g���z��
�ƂȂ�C����ɂ���1���������C����f��
���z��
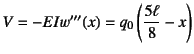 �ƂȂ�B
���������`��Ƌ��ɐ}�������̂��}-4.11�ł���B
������C���[�̎x�_���̓��[�����g�͎�(4.32)��
�ƂȂ�B
���������`��Ƌ��ɐ}�������̂��}-4.11�ł���B
������C���[�̎x�_���̓��[�����g�͎�(4.32)��![]() �������āC
���E������(4.28c)�̕����ɋC��t�����
�������āC
���E������(4.28c)�̕����ɋC��t�����
�ƂȂ�B�܂���̂���f�͂�![]() ,
, ![]() �������āC
��������E������(4.28b)�̕����ɋC��t�����
�������āC
��������E������(4.28b)�̕����ɋC��t�����
�Ƌ��߂���B ���̂悤�ɁC�\���S�̂̕ό`�����߂�ꂽ���ƂŎx�_���͂����߂��邱�ƂɂȂ�B �Ȃ����[�����g�}�Ƃ���f�͐}�̍��E�[�̒l�Ɣ��͂̒l�̕����̈Ⴂ�ɂ� �\�����ӂ��邱�ƁB
����
���͐}-4.12�̗��[�Œ�̗��ł���B
���E�����͗��[��
�ƂȂ�B���z�O�͏����͑O�̗��Ɠ����Ȃ̂ŁC��ʉ���
��(4.30)�Ɠ����ł���B�܂����[�̋��E�����������Ȃ̂ŁC
���ԓI�ȉ��̕\���Ƃ���
�ƒu���Ă����B����Ƃ���1�K�̔��W���Ƃ��E�[�̋��E������
��������
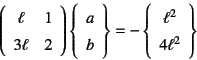
��B
����������Ό���![]() ,
, ![]() �ƂȂ�C����݂�
�ƂȂ�C����݂�
�ƂȂ�B����2�K�̔��W������Ȃ����[�����g���z��
���邱�Ƃ��ł��邪�C���ɒ[���̕s�Ò胂�[�����g��
�ƂȂ�B�܂��x�_���͂�
�ƂȂ�B ����͎��́C�\�������E�Ώ̂Ȃ̂ŐÒ�n�Ɠ����悤�ɗ͂̂荇���ł� ���߂���B�}-4.13�Ɋe�}�������Ă������B �ȏ�̓�̌��ʂ̐}-4.11, 4.13����� ���炩�Ȃ悤�ɁC1�X�p���̕s�Ò���̏ꍇ�ɂ́C���[�̕s�Ò� ���[�����g�����߂�������C����ɐÒ���̋Ȃ����[�����g ���z���d�ˍ��킹�邱�Ƃɂ���ē��邱�Ƃ��ł���B ���̂悤�ȁC�d�ˍ��킹�ɂ���@�ɂ��Ă͌�q���邪�C�s�Ò胂�[�����g�� ���߂邾���Ȃ��-5�ʼn��������@���֗��ł���C ���݂ł͎��p�I�ɂ��L���p�����Ă���B ���j�I�ɂ͑��ɂ��������̎�@���l�Ă���Ă������C ���̕����ł͂����������ÓT�I�ȕ��@�ɂ��Ă͓K�Ɏ�̑I�������B �ȏ�̂悤�ɕs�Ò�\���̏ꍇ�ɂ́C�ψʂ𖢒m���Ƃ��� ���E�l�����������Ƃɂ���āC���̎x�_���͂�s�Ò� ���[�����g����ыȂ����[�����g���z�������߂邱�Ƃ��ł��邱�Ƃ� �������Ă��炦���Ǝv���B
����C�Ò�\���̏ꍇ�͋Ȃ����[�����g���z���ȒP�ɎZ��ł���̂ŁC
����݂𖢒m���Ƃ���4�K�̔�����������������n�߂�K�v�͖����B
�����������������B�}-4.14��
�ł���{�I�ȐÒ���ł���B
���̏ꍇ�͏�-2�Ń��[�����g���z�����߂��Ă���
�ƂȂ��Ă���B���������Ď�(4.27b)�̂荇����
�܂ők�炸�Ƃ��C��(4.13b)�̋Ȃ����[�����g��
�ȗ��̊W�ɏ�̃��[�����g���z������������B�܂�
�����������B
���[�̊w�I���E�����͋���![]() �ł��邩��C
�㎮��2��ϕ�������ʉ�
�ł��邩��C
�㎮��2��ϕ�������ʉ�
�����E�����ɑ�������
![]() ,
,
![]() �ƂȂ�C����݂�
�ƂȂ�C����݂�
�Ƌ��߂���B1���������ƁC���ɗ��[�̂���݊p��
�ƂȂ��Ă���B�}-4.15�� ����`����������B
���̗����\�I�ȐÒ�\���ŁC��[�ɂ���f�O�͂�
��p�����}-4.16�̕Ў������ł���B
�Ȃ����[�����g���z��![]() �ł��邩��C
�����2��ϕ����Đϕ��萔�����[�̊w�I���E��������
���肷��ƁC����݂͍ŏI�I��
�ł��邩��C
�����2��ϕ����Đϕ��萔�����[�̊w�I���E��������
���肷��ƁC����݂͍ŏI�I��
�ƂȂ�B��[�̂���݂Ƃ���݊p��
(4.37)
�ƂȂ��Ă���B�}-4.17�ɂ͂���`��݂̂��������B
���邢�́C��[�ɏW���O�̓��[�����g����p�����ꍇ�ɂ́C
���[�����g���z��![]() �ƈ��ɂȂ�̂ł����
�ȒP�ɔ����������������C�Ǒ��̊w�I���E�����ɑ�����邱�Ƃ�
����Ă���݂�
�ƈ��ɂȂ�̂ł����
�ȒP�ɔ����������������C�Ǒ��̊w�I���E�����ɑ�����邱�Ƃ�
����Ă���݂�
�Ƌ��߂���B��[�̂���݊p�͂��̔��W�����
�Ƌ��߂���B����`���}-4.18�Ɏ������B
���̗�͐}-4.19�ɂ���悤�ɁC
�P�����̍��[�ɏW�����[�����g���������ꍇ�ł���B
������Ò�\���ł���C�Ȃ����[�����g
���z��
![]() ��
���߂��B������Ȃ����[�����g�Ƃ���݂�
�W�ɑ�����Ĕ����������������C���[�ł���݂���ɂȂ������
�ϕ��萔�����߂�C�ŏI�I�ɂ���݂̉���
��
���߂��B������Ȃ����[�����g�Ƃ���݂�
�W�ɑ�����Ĕ����������������C���[�ł���݂���ɂȂ������
�ϕ��萔�����߂�C�ŏI�I�ɂ���݂̉���
�ƂȂ�B1���������ƁC���[�̂���݊p��
�ƎZ�肳���B�}-4.20�ɂ���`��������Ă������B �Ò�n�Ȃ̂Ŏx�_���͂͂荇�����ŋ��߂���B
�Ō�ɒe���x�����ꂽ�}-4.21�̕s�Ò���������Ă������B
��ʉ��͎�(4.30)��
�����ɂȂ�C�E�[�̗͊w�I���E��������(4.29)��
�\������邱�Ƃɒ��ӂ���������C���E������
�ł���B�ȏ�̎l�̏����Ɉ�ʉ����������![]() ��
��
�Ƃ����W�C�����������
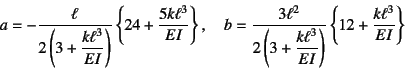
��B������o�l�x�����ꂽ�_�̂���݂����߂��
�ƂȂ�B������
���e���x���o�l�̉e�����\���閳�����p�����[�^�ł���B
�x�_���͓͂���ꂽ�����![]() �̔��W�������߂�Όv�Z���邱�Ƃ��ł��邪�C
�����ł͏ȗ�����B
�e���x���Ƃ����͍ŏ��͂��܂藝���ł��Ȃ���������Ȃ����C
���ۂ̎x���������ώ@�����ꍇ�ɁC��قNj��łȊ�Ղɒ��ڐݒu���ꂽ
�x���łȂ�����C�d�ɂ���Ă͈ꎞ�I�ɒ�������x�����������݂���B
��������C���łȒn�ՁE��ՂŎx������Ă��Ȃ�������
�ߎ��I�Ƀ��f��������悤�ȏꍇ���ɂ��C
���̒e���x���Ƃ��������͗p�����邱�Ƃ����邱�Ƃ͊o���Ă����ė~�����B
�̔��W�������߂�Όv�Z���邱�Ƃ��ł��邪�C
�����ł͏ȗ�����B
�e���x���Ƃ����͍ŏ��͂��܂藝���ł��Ȃ���������Ȃ����C
���ۂ̎x���������ώ@�����ꍇ�ɁC��قNj��łȊ�Ղɒ��ڐݒu���ꂽ
�x���łȂ�����C�d�ɂ���Ă͈ꎞ�I�ɒ�������x�����������݂���B
��������C���łȒn�ՁE��ՂŎx������Ă��Ȃ�������
�ߎ��I�Ƀ��f��������悤�ȏꍇ���ɂ��C
���̒e���x���Ƃ��������͗p�����邱�Ƃ����邱�Ƃ͊o���Ă����ė~�����B
�ɂȂ邪�C����͎�(4.40)�ɂ�����
�x���o�l�W�����܂�![]() ���邢��
���邢��![]() �Ƃ������ł�
����B
�Ƃ������ł�
����B
�ƂȂ��Ă��邱�Ƃ������B
�Ō�ɁC��(4.23)�ł͏ڂ����͐������Ȃ�����
���E�����̑g�ݍ��킹���ɂ��Ă���ɗ�����[�߂邽�߂ɁC
�ȒP�ȗ�������Ă������B
����͐}-4.24�ɂ���悤�ɁC���݂���
�荇�������͓��m�����[�ɍ�p���Ă��钌�ł���B���̏ꍇ��
���E������
�ƂȂ�B����C�������ψ�![]() �ŕ\�����荇������
��(4.27a)��
�ŕ\�����荇������
��(4.27a)��![]() ���ƒu�������̂ł��邩��C
���̈�ʉ���
���ƒu�������̂ł��邩��C
���̈�ʉ���![]() �ł����B
��̋��E�����ɂ���������ē�̐ϕ��萔
�ł����B
��̋��E�����ɂ���������ē�̐ϕ��萔![]() ,
, ![]() ��
���߂悤�Ƃ��Ă��C�ŏI�I�ɂ�
��
���߂悤�Ƃ��Ă��C�ŏI�I�ɂ�
�ƂȂ��Ă��܂��B
����͉������݂��Ȃ��̂ł͂Ȃ������ɑ��݂��邱�Ƃ�
�Ӗ����Ă���B�܂�C���̒��͑��ΓI�ɏk��ł����
�i�㎮![]() �̑�2����
�̑�2����
![]() ��
�k�݂Ђ��݂ŁC
��
�k�݂Ђ��݂ŁC
![]() �����[�ɑ��鑊�ΓI�ȏk�ݕψʁj�C
���������̂ǂ̈ʒu�ɍ��̓I�Ɉړ��i�㎮��
�����[�ɑ��鑊�ΓI�ȏk�ݕψʁj�C
���������̂ǂ̈ʒu�ɍ��̓I�Ɉړ��i�㎮��![]() �j���Ă��C
���̈ʒu�ł荇���ĐÎ~�ł��邱�Ƃ������Ă���ɉ߂��Ȃ��B
�܂����E�̎��͂��قȂ�ꍇ�ɂ͉������݂��Ȃ��i�O�͓��m����
�荇���Ă��Ȃ��̂����瓖�R�ŁC�^�����Ă��܂��j���Ƃ��킩��B
�j�����C
���̈ʒu�ł荇���ĐÎ~�ł��邱�Ƃ������Ă���ɉ߂��Ȃ��B
�܂����E�̎��͂��قȂ�ꍇ�ɂ͉������݂��Ȃ��i�O�͓��m����
�荇���Ă��Ȃ��̂����瓖�R�ŁC�^�����Ă��܂��j���Ƃ��킩��B
���Ȃ킿�C���E��������(4.28)�̂悤�ȎO�̑g�ݍ��킹�� �^������K�v�������ɁC���[�ł����̗^���������Ȃ��� �����B��ł͂Ȃ������葶�݂��Ȃ��Ȃ����肷�邱�Ƃɏ\�����ӂ���K�v������B ��̓I�ɂ́C���[�̋��E�����̒��ɕK�� �w�I���E�������K���^���Ă����K�v������B ���l�v�Z���ł́C���E�����̗^�����œ��̓~�X������ƌ��ʂ� �o�Ȃ����Ƃ�����̂Œ��ӂ��K�v�ł���B ��ʘ_�Ƃ��āC�������݂��邩�ۂ��C���݂���ꍇ�ɗB��ł��邩�ǂ��� �ɂ��ẮC��-5.4.2�ł��Ꭶ����B