 |
前節で扱った変形は 幾何学的に明確に定義できる量ではあったが, 材料の抵抗という観点から物理的な意味がわかり易い変形を どれにすればいいのかについては,結構難しい課題であった。 実は応力の定義においても同様の困難が伴う。 そもそも応力が必要になる理由は,一つはNewtonの法則つまり つり合い式を力で書いた方がわかり易いからだ。 材料は「変形して」抵抗するが,その変形で直接つり合いを考えるよりも, それに対応した「抵抗力」でつり合いを考えた方がわかり易いからだ。 もう一つの理由は,材料の抵抗の仕方つまり構成則を,「抵抗力」と「変形」の 間の関係で定義するという手法が,ちょうどバネの抵抗則と同じように わかり易くなるからだ。 いずれにしても単なる数学的な量・概念であるから, 使い易いように好きに自由に定義すればいいことになる。 そのように考えると,変形した現配置において作用している外力に 対して材料は抵抗しているのだから,Euler的な応力でつり合いを表すのが 素直なように思えてくる。 しかし構成則は,ある物質点がどのような履歴を経て抵抗してきたかということを 表すべきだろうから,これについてはLagrange的な応力を定義しておいた方が いいように感じられる。 どっちがいいだろう。 そこでここでは,代表的な二つの応力を定義し,その間の関係を求めておこう。
さて応力は,物体内に仮想的に定義した面に生じている抵抗力を,
その面の面積で割った圧力のような量だった。
問題は,どの配置でその面と面積を定義するのか,さらにどの物質点に
着目しているのか,そしてどの座標系でその成分を捉えようとしているか,
という点でそれぞれ複数の選択が可能になることだ。
そこでまず,現配置において単位面積を定義して,
その面に生じている抵抗力を,
空間固定座標方向の応力として定義しよう。
これはEuler的な応力の定義になり,これはちょうど
微小変形理論の式(3.19)と図-3.10で
定義した応力と同じような定義になる。
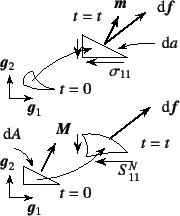
つまり図-12.7の上に示したような![]() の
微分面積
の
微分面積![]() に
発生した抵抗力ベクトル
に
発生した抵抗力ベクトル![]() で表面力ベクトル
で表面力ベクトル![]() を
を
と定義した上で,この表面力ベクトルの空間固定基底ベクトル方向成分を,
その抵抗力が発生している面の法線ベクトル![]() を用いて
を用いて
のように定義して,Cauchy応力(真応力)
![]() を定義する。
実はこの定義はとてもわかり難いはずだ。
法線方向から力への射影が応力になっているからだ。
幾何学的・物理的に理解するためには,
微小変形理論の図-3.10の方がいい。
それをカッコ良く式にしたのが上の定義だと考えておいた方が健康的だ。
なお,添え字の定義は図-3.11と式(3.19)と
同じ12.12である。
を定義する。
実はこの定義はとてもわかり難いはずだ。
法線方向から力への射影が応力になっているからだ。
幾何学的・物理的に理解するためには,
微小変形理論の図-3.10の方がいい。
それをカッコ良く式にしたのが上の定義だと考えておいた方が健康的だ。
なお,添え字の定義は図-3.11と式(3.19)と
同じ12.12である。
一方,鋼の引張り試験で応力ひずみ曲線を描くときのように,
試験機で測定した荷重を初期配置で測定した断面積で割って定義した応力も
必要かもしれない。
そういったLagrange的な応力は,図-12.7の下に
示したように,初期配置で![]() であった面が現配置の位置に
移動して,そこに
であった面が現配置の位置に
移動して,そこに![]() が
発生して抵抗しているとみなせばいい。
が
発生して抵抗しているとみなせばいい。![]() が
発生している「物質点」は上のCauchy応力を定義した「場所」と
同じにしたが,面積を初期配置に戻って定義し直したと考えればいい。
つまり式(12.75)に対応させて
が
発生している「物質点」は上のCauchy応力を定義した「場所」と
同じにしたが,面積を初期配置に戻って定義し直したと考えればいい。
つまり式(12.75)に対応させて
のようにnominal応力
![]() が定義12.13できる。
ここに
が定義12.13できる。
ここに![]() は,初期配置における面
は,初期配置における面![]() の法線ベクトルである。
つまり現配置で生じている表面力を初期配置の単位面積で定義した
空間固定座標方向の応力になっている。
もう少し詳しい物理的な意味はあとでまとめて説明しよう。
の法線ベクトルである。
つまり現配置で生じている表面力を初期配置の単位面積で定義した
空間固定座標方向の応力になっている。
もう少し詳しい物理的な意味はあとでまとめて説明しよう。
さてここで,初期配置の面積と現配置の面積との対応を求めておこう。
初期配置の微分面積![]() は
は
と定義できる。
ここに![]() は式(J.15)で定義した交代記号である。
一方,現配置の微分面積
は式(J.15)で定義した交代記号である。
一方,現配置の微分面積![]() も同様に
も同様に
と定義できるが,これは同じ物質点近傍の面積なので,変形勾配を用いると
と関係付けられる。
最後の式の括弧の中は![]() を故意にこのように書いてある。
すると,式(12.13)のJacobianを用いて
を故意にこのように書いてある。
すると,式(12.13)のJacobianを用いて
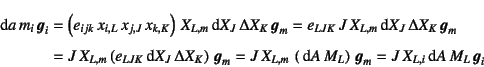
という関係が得られることから,変形前後の面積は
という関係にあることがわかる。
この式(12.79)を式(12.75)に代入し,
式(12.76)と等値すれば
となるから,二つの応力間の関係が
のように求められる。
テンソルの直接表記と称して,よく
と書かれることがあるが,応力成分の最初の添え字が面積の法線を 定義する基底ベクトルを表して12.14おり,二つ目の添え字が応力の向きを定義する 基底ベクトルを表している。
Cauchy応力で表したつり合い式(運動方程式)は,
微小変形理論のそれと同じになるのは明らかである。
つまり,式(3.22)と
同じく
である。ここに,
![]() は単位質量当たりの
分布外力であり,
は単位質量当たりの
分布外力であり,
![]() は加速度で,
式(12.62)で表されるように移流項があることを忘れてはいけない。
また境界条件は,
は加速度で,
式(12.62)で表されるように移流項があることを忘れてはいけない。
また境界条件は,![]() が物体境界面の法線ベクトルだとみなすと
が物体境界面の法線ベクトルだとみなすと
となる。ここに
![]() は現配置における単位面積当たりの
表面外力である。
また,モーメントのつり合いも微小変形理論のそれと同じなので
は現配置における単位面積当たりの
表面外力である。
また,モーメントのつり合いも微小変形理論のそれと同じなので
となるから,Cauchy応力は対称テンソルである。
さて,運動量保存則は
となるだろうから,![]() を単位質量当たりの内部エネルギ率とすると,
これは
を単位質量当たりの内部エネルギ率とすると,
これは
と表すことができる。ここに,
![]() は物体内の
熱源からの分布熱量速度であり,
は物体内の
熱源からの分布熱量速度であり,
![]() は現配置における
表面外向きの熱流率である。
熱成分を無視した場合,
式(12.14)の質量保存則
は現配置における
表面外向きの熱流率である。
熱成分を無視した場合,
式(12.14)の質量保存則
![]() を念頭に置けば,
最初の2項は単純に物質微分でき
を念頭に置けば,
最初の2項は単純に物質微分でき
となる。これに式(12.82)のつり合い式を代入して
分布外力![]() を
消去し,Gaussの発散定理を用いたあと,式(12.83)の境界条件を
代入すれば
を
消去し,Gaussの発散定理を用いたあと,式(12.83)の境界条件を
代入すれば![]() が無くなり,最終的に
が無くなり,最終的に
となる。これより単位質量当たりの内部エネルギ率は
と書くこともできるので,
モーメントのつり合い式(12.84)を用いて結局
と表すことができる。ここに![]() は変形速度であり,
右辺
は変形速度であり,
右辺![]() は応力の仕事率
である。熱成分が含まれる場合も同様に定式化でき
は応力の仕事率
である。熱成分が含まれる場合も同様に定式化でき
となり,応力の仕事率と熱の仕事率成分の和になる。
式(12.86)から,Cauchy応力![]() は
変形速度
は
変形速度![]() と「対」になっていることがわかる。
この情報は,構成則を与えるときに参考になる重要なものである。
と「対」になっていることがわかる。
この情報は,構成則を与えるときに参考になる重要なものである。
あるいはLagrange的に見直すと,熱成分を無視した式(12.85)は
と書くことができる。
ここに![]() は変形前の
単位面積当たりの初期配置を基準配置とする表面力であるが,
向きは空間固定基底ベクトルで規定されているものとする。
また分布外力は同じ
は変形前の
単位面積当たりの初期配置を基準配置とする表面力であるが,
向きは空間固定基底ベクトルで規定されているものとする。
また分布外力は同じ![]() という記号を用いているが,
正確には
という記号を用いているが,
正確には
![]() ,つまり物質点
,つまり物質点![]() の関数である。
そのように考えると,nominal応力の定義式(12.76)からも
容易に類推できるように,法線ベクトル
の関数である。
そのように考えると,nominal応力の定義式(12.76)からも
容易に類推できるように,法線ベクトル![]() を持つ物体表面の力の境界条件は
式(12.83)と同様,nominal応力を用いて
を持つ物体表面の力の境界条件は
式(12.83)と同様,nominal応力を用いて
と与えることができる。この式(12.89)を
式(12.88)に代入してGaussの発散定理を用いると,結局
となる。これからLagrange的なつり合い式
は,nominal応力を用いて
と表すことができ,応力の仕事率が
と表される。したがって,nominal応力![]() は
変形速度
は
変形速度![]() とではなく,Lagrange的な
速度勾配
とではなく,Lagrange的な
速度勾配![]() と「対」になっていることがわかる。
式(12.90)のつり合い式は,
式(12.82)のCauchy応力で表したものと非常によく似ているが,
微分を物体の「物質点」
と「対」になっていることがわかる。
式(12.90)のつり合い式は,
式(12.82)のCauchy応力で表したものと非常によく似ているが,
微分を物体の「物質点」![]() で行っているように,
全く異なる観点から見たつり合い式である。
で行っているように,
全く異なる観点から見たつり合い式である。
また,式(12.80)の関係をCauchy応力のモーメントの
つり合い式(12.84)に代入すれば,nominal応力の
モーメントのつり合いは
としか表すことができないので,nominal応力![]() は
非対称テンソルであることがわかる。
念のために,節-3.2.5と
同じ演算をして,静的なモーメントのつり合いをとっておこう。
全外力のモーメントのつり合いは
は
非対称テンソルであることがわかる。
念のために,節-3.2.5と
同じ演算をして,静的なモーメントのつり合いをとっておこう。
全外力のモーメントのつり合いは
となる。上式第1項の![]() に境界条件式(12.89)を代入すると
に境界条件式(12.89)を代入すると
となるので,Gaussの発散定理を用いれば
すなわち
となる。これに,慣性項を無視した
つり合い式(12.90)を代入すると,結局,
第1項の被積分関数の第1項以外は無くなって
となることから,モーメントの つり合い式(12.92)を,被積分関数に得る。
あといくつか重要な応力を定義しておこう。
まずKirchhoff応力
![]() は,応力の仕事率の表現で
は,応力の仕事率の表現で
という関係で定義される。つまり,
である。 ただし,基準配置は現配置であることに注意する。 少し奇妙な応力で,使い方はよくわからない。
これによく似た応力テンソルで初期配置を基準配置とするLagrange的な応力を
次に定義する。
変形速度を定義した式(12.52)から
という関係を得るので,これを応力の仕事率の表現式(12.86)に
代入すると
と書くこともできる。
この括弧の中を新しい応力テンソル
![]() として定義することにすれば,
結局
として定義することにすれば,
結局
のように応力の仕事率を表現できることになる。
この
![]() は第2 Piola-Kirchhoff応力
と呼ばれ
は第2 Piola-Kirchhoff応力
と呼ばれ
と定義される。
注意しないといけないのは,もはや![]() は単位直交基底では
なくなっていることである。
したがって,ちょうど節-J.4で示した
極座標の例のように,物理的な成分とテンソル成分
は単位直交基底では
なくなっていることである。
したがって,ちょうど節-J.4で示した
極座標の例のように,物理的な成分とテンソル成分![]() との
違いを明確にしておくことが重要になる。
また同じ理由で,第2 Piola-Kirchhoff応力とnominal応力では
共変成分と反変成分を区別する必要があるが,
この章の議論で特にそれが必要になることは無いので,以下も
下添え字を用いることにする。
また構成則を考えるときには,第2 Piola-Kirchhoff応力はGreenのひずみと
関連付けることが望ましいことを,
上式の応力の仕事率の「組」は示唆している。
との
違いを明確にしておくことが重要になる。
また同じ理由で,第2 Piola-Kirchhoff応力とnominal応力では
共変成分と反変成分を区別する必要があるが,
この章の議論で特にそれが必要になることは無いので,以下も
下添え字を用いることにする。
また構成則を考えるときには,第2 Piola-Kirchhoff応力はGreenのひずみと
関連付けることが望ましいことを,
上式の応力の仕事率の「組」は示唆している。
さて,式(12.97)に
式(12.80)のnominal応力とCauchy応力の関係を代入すれば
という関係にあることがわかる。これと式(12.97)を
見比べながら,
もう一つ応力テンソルを定義したのが,第1 Piola-Kirchhoff応力
である。それを![]() と記し
と記し
と定義する。つまり
という関係にある。ちょうどnominal応力の「転置」のように見えるが, 物理的な意味は異なるので注意が必要である。
最後に,第2 Piola-Kirchhoff応力で
表したつり合い式は,nominal応力との
関係式(12.98)を式(12.90)に代入することによって
となる。
注意しなければならないのは,このつり合い式は式(12.90)と同様,
微分を物体の「物質点」毎に行っていることである。
したがって分布外力も
![]() である。
しかし,そのつり合いは空間固定基底の
である。
しかし,そのつり合いは空間固定基底の![]() 方向で
表示してあることにも注意すべきである。
第2 Piola-Kirchhoff応力が
方向で
表示してあることにも注意すべきである。
第2 Piola-Kirchhoff応力が![]() 方向の力であることから,
一種の座標変換である変形勾配
方向の力であることから,
一種の座標変換である変形勾配
![]() が乗じられた成分で
つり合いを表現している。
が乗じられた成分で
つり合いを表現している。
最後に,式(12.44)の伸びひずみあるいはBiotのひずみ![]() と
組になる応力[59]を定義しておく。
式(12.9) (12.18) (12.44)から
と
組になる応力[59]を定義しておく。
式(12.9) (12.18) (12.44)から
となることを式(12.96)に代入し,
式(12.44)の定義から
![]() で
あることを念頭に置いて,
で
あることを念頭に置いて,![]() と
と![]() が対称テンソルで
あることを用いて,最終的に
が対称テンソルで
あることを用いて,最終的に
![]() と組になる応力が
対称テンソルになるように注意して演算すると
と組になる応力が
対称テンソルになるように注意して演算すると
となることから,新しい応力テンソルが
と定義できる。この
![]() はBiot応力
と呼ばれる。
念のために,応力の仕事率の組み合わせをまとめておくと次のようになる。
はBiot応力
と呼ばれる。
念のために,応力の仕事率の組み合わせをまとめておくと次のようになる。
ところで上では対称な応力テンソルとして定義したが,同じ演算で非対称の
のようなテンソルとしても定義できる。これを式(12.98)に
代入すると,極分解の定理を用いることによって,nominal応力との間に
という関係が成り立つ。nominal応力![]() が空間固定座標方向の成分を持つ
ことを念頭に置くと,Biot応力は,初期配置の単位面積当りの
埋め込み座標基底の現配置の単位基底方向成分であることがわかる。
これがBiot応力の物理的な意味であろう。
が空間固定座標方向の成分を持つ
ことを念頭に置くと,Biot応力は,初期配置の単位面積当りの
埋め込み座標基底の現配置の単位基底方向成分であることがわかる。
これがBiot応力の物理的な意味であろう。
節-E.2で定式化したBernoulli-Euler梁の
有限変位の枠組でのつり合い式では,
第2 Piola-Kirchhoff応力が用いられ,幾何学的にもわかり易い理論が
構築されている。
それを例にして第2 Piola-Kirchhoff応力とGreenのひずみの
物理的な意味を説明しよう。まず式(12.103)の
ペアと同様,仮想仕事式が式(E.21)の
のようになり,式(E.22)で定義し直した第2 Piola-Kirchhoff応力の
物理成分
と,式(E.19)で定義されるGreenのひずみの物理成分としての伸び
の積で,内部仮想仕事が算定できている。![]() はCauchy応力では
ない。
はCauchy応力では
ない。![]() が
が![]() 方向の
応力成分であり,基底ベクトルは単位ではなく
方向の
応力成分であり,基底ベクトルは単位ではなく
![]() であることがわかれば
であることがわかれば
であるから,![]() が
が![]() の物理的に意味のある成分であり値であることが
明らかだ。
また変形前に単位量だった梁の軸方向の基底ベクトル
の物理的に意味のある成分であり値であることが
明らかだ。
また変形前に単位量だった梁の軸方向の基底ベクトル![]() が伸びて,
変形後に
が伸びて,
変形後に![]() になっているから,
になっているから,
![]() が
軸線の伸びであることも明らかだ。つまり,
が
軸線の伸びであることも明らかだ。つまり,![]() はGreenのひずみ
はGreenのひずみ![]() の
物理成分であり,
上式の定義は式(12.24a)と同じであり,
実はそれは式(12.44)の伸びひずみテンソル
の
物理成分であり,
上式の定義は式(12.24a)と同じであり,
実はそれは式(12.44)の伸びひずみテンソル![]() の
成分に一致する。
そして梁の構成則は上記の仮想仕事式の組を念頭に置いて
の
成分に一致する。
そして梁の構成則は上記の仮想仕事式の組を念頭に置いて
とモデル化することによって,とても美しい理論が構築できる。
さらにつり合い式(E.27)は,
少し書き換えると
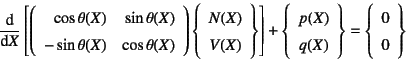
となる。軸力![]() はたわんで
はたわんで![]() 回転した軸線方向の力であり,
せん断力
回転した軸線方向の力であり,
せん断力![]() はそれに直交した方向の力である。
つまり内力は
はそれに直交した方向の力である。
つまり内力は![]() 方向の力である。
しかし外力
方向の力である。
しかし外力![]() と
と![]() は空間固定座標の
は空間固定座標の![]() 方向で
定義されているため,
たわみ角
方向で
定義されているため,
たわみ角![]() で定義できる座標変換行列を断面力に乗じて
空間固定座標方向に変換したつり合い式になっているのである。
この座標変換行列の部分が
上式(12.101)の
で定義できる座標変換行列を断面力に乗じて
空間固定座標方向に変換したつり合い式になっているのである。
この座標変換行列の部分が
上式(12.101)の
![]() に相当する。
そして微分は物質点座標
に相当する。
そして微分は物質点座標![]() でとってある。
ちなみに外力
でとってある。
ちなみに外力![]() も
も![]() も物質点座標(変形前の座標)
も物質点座標(変形前の座標)![]() の関数として定義されている。
の関数として定義されている。
これまでの定義はやや数学的過ぎたので,図-12.8を 用いて物理的な意味を整理しておこう。
 :
初期配置の単位面積を追跡して現配置に至った面に発生した内力表面ベクトルの,
現配置における物体埋め込み座標の「単位」基底ベクトル方向の成分を持つ
応力テンソルに相当する。
:
初期配置の単位面積を追跡して現配置に至った面に発生した内力表面ベクトルの,
現配置における物体埋め込み座標の「単位」基底ベクトル方向の成分を持つ
応力テンソルに相当する。
簡単な例として,図-12.2つまり図-12.9の
ように3方向にそれぞれストレッチ![]() (
(![]() , 2, 3)だけが
生じて
, 2, 3)だけが
生じて![]() -
-![]() 面内で
面内で![]() だけ剛体的に回転した
状態で,
だけ剛体的に回転した
状態で,
![]() 方向にのみ
内力表面力
方向にのみ
内力表面力![]() が発生しているものとする。
こうしておけば,どの応力テンソルでも,成分同士の直交性・平行性が
成り立つので考え易い。
一般に鋼の引張り試験等,初期状態の寸法がわかっている状態で
試験機で測定できる反力から応力を推定しているので,
このように初期状態で単位面積を持った面に,初期の単位面積当たりの内力表面力
が発生しているものとする。
こうしておけば,どの応力テンソルでも,成分同士の直交性・平行性が
成り立つので考え易い。
一般に鋼の引張り試験等,初期状態の寸法がわかっている状態で
試験機で測定できる反力から応力を推定しているので,
このように初期状態で単位面積を持った面に,初期の単位面積当たりの内力表面力![]() が現配置において
生じている状況を考えている。
もちろん普通の試験片ではここで考えているような
巨視的な回転
が現配置において
生じている状況を考えている。
もちろん普通の試験片ではここで考えているような
巨視的な回転![]() はほとんど無いと考えられるが,有限変形をする物体の場合,
物体のある箇所の大変形が他の箇所への剛体回転を生むことは大いに
あり得ることから,ここでも考慮してある。
この例では埋め込んだ
はほとんど無いと考えられるが,有限変形をする物体の場合,
物体のある箇所の大変形が他の箇所への剛体回転を生むことは大いに
あり得ることから,ここでも考慮してある。
この例では埋め込んだ![]() 方向にしか内力表面力が
発生していないので,第2 Piola-Kirchhoff応力は簡単に誘導できる。
ただ注意しないといけないのは,この成分は
方向にしか内力表面力が
発生していないので,第2 Piola-Kirchhoff応力は簡単に誘導できる。
ただ注意しないといけないのは,この成分は![]() 方向成分で
あることであり,その基底ベクトルと合わせて
方向成分で
あることであり,その基底ベクトルと合わせて
とならなければならないことである。![]() が単位基底ベクトルでは
ないから,ストレッチ
が単位基底ベクトルでは
ないから,ストレッチ
![]() を用いて
を用いて
となる。![]() は第2 Piola-Kirchhoff応力
は第2 Piola-Kirchhoff応力![]() の物理成分と
呼ばれることもあり,値も単位も実際の圧力である。
そしてBiot応力は式(12.102)から
の物理成分と
呼ばれることもあり,値も単位も実際の圧力である。
そしてBiot応力は式(12.102)から
となり,Lagrange的な物理的に意味のある応力であることがわかる。
これに対し,nominal応力は同じ面に発生した表面力の
空間固定座標![]() 方向の成分であるから,単純に
方向の成分であるから,単純に
となる。
次に![]() を第2 Piola-Kirchhoff応力として扱いながら,Cauchy応力を
求めてみよう。Cauchy応力は現配置の単位面積当たりの応力であるから,
同図の右から2番目の図に示した内力が発生している面とのつり合いから
を第2 Piola-Kirchhoff応力として扱いながら,Cauchy応力を
求めてみよう。Cauchy応力は現配置の単位面積当たりの応力であるから,
同図の右から2番目の図に示した内力が発生している面とのつり合いから
という関係にある。Cauchy応力は現配置における単位面積当たりの
力であることと,![]() の定義によって右辺には現配置での
面積
の定義によって右辺には現配置での
面積
![]() が無いこととに注意する。
ここが第2 Piola-Kirchhoff応力について最もわかり難いところ12.15である。
同様に一番右の図に示した上面(自由表面)とのつり合いから
が無いこととに注意する。
ここが第2 Piola-Kirchhoff応力について最もわかり難いところ12.15である。
同様に一番右の図に示した上面(自由表面)とのつり合いから
つまり
となるので,上の式(![]() )に代入することによってCauchy応力が
)に代入することによってCauchy応力が
と算定できる。求めてしまえば当たり前だろう。
というのも,右辺の
![]() が
右の面に生じているCauchy応力の
が
右の面に生じているCauchy応力の
![]() 方向
成分であるから,この式は単に座標変換式(3.37)を
示しているに過ぎないからである。
方向
成分であるから,この式は単に座標変換式(3.37)を
示しているに過ぎないからである。
最後に第1 Piola-Kirchhoff応力を求めてみよう。
まず,質量保存則から
であるから,上式のCauchy応力に対するKirchhoff応力は,
その定義式(12.94)から
となる。これはあまりよくわからない成分である。
次に,法線が![]() になる面のKirchhoff的表面力
になる面のKirchhoff的表面力![]() は
は
であり,これを
![]() 方向
成分
方向
成分
![]() と
と
![]() 方向
成分
方向
成分
![]() に分解すると
に分解すると
と等値されるはずなので
となる。最後にこれを第1 Piola-Kirchhoff応力で表すと
と等値されなければならないので,結局
と求められる。同じ演算を法線が![]() になる面の表面力に
対して行うと
になる面の表面力に
対して行うと
であることから
となる。以上の結果をまとめると
と求められる。確かにnominal応力成分と転置の関係にあるが,力の 向きや発生している面が異なるから,値が転置の関係にあるだけのことである。
さて,各種応力テンソル間の関係式から成分を誘導し,
ここまでに力学的・幾何学的に求められた成分が正しいかどうかを確認しよう。
ここの例は図-12.2と同じく3軸方向へのストレッチと
回転のみの簡単な運動なので式(12.34)と同様
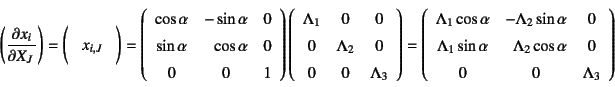
となる。
これを用いて,Cauchy応力と第2 Piola-Kirchhoff応力の
関係式(12.97)に
式(12.105)を代入してCauchy応力を求めてみよう。
密度比が式(![]() )であることに注意すれば
)であることに注意すれば
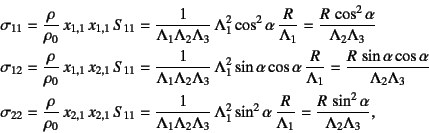
となり,これは式(12.107)に一致する。
次に,式(12.105)の
第2 Piola-Kirchhoff応力を式(12.99)に代入して
第1 Piola-Kirchhoff応力を求めてみると,零でない成分は
となり,これは式(12.109)に一致する。
また同様に,式(12.76)でnominal応力を求めてみると,
零でない成分は
となり,これも式(12.106)に一致する。
ところで,鋼の引張り試験結果を図示するときに,ロードセルの読みを 試験片の初期状態の断面積で割った「応力」を公称応力 と呼んで用いることがある。 いわゆる「絞り」が発生するまでの間は真応力と工学的には差異が無いことが多い。 ときどき,この公称応力が第1 Piola-Kirchhoff応力であると 言われるようだが,図-12.10のように せん断帯(Lüders帯) が出たあとの若干回転した試験片の状況を考えると, 公称応力は空間固定座標方向の応力であることがわかるので, どちらかと言えばnominal応力の方12.16に近いと考えざるを得ない。 実際,公称応力は`nominal stress'と訳される12.17ことが多い。 ただし,公称応力が9成分を持つ非対称応力テンソルだという 認識は無いと考え,この文書では公称応力という名称は用いない。
さて,ここまでの段階で各応力の物理的な違いが明確には理解できなかった人は たくさんいるだろう。 むしろ,その人数の方が多いと思うので,がっかりする必要は無い。 しかし,本当にもし理解が不十分だと感じている読者は, そのままでは,この先に進まない方がいい。きっと怪我をします。
さて,有限変形を許容するということは,塑性変形も生じるのが
一般的であると考えていい。
そのとき流れ則を規定しなければならないことから,少なくとも
変形(ひずみ)は増分あるいは速度で表現できないといけなかった。
それに対応した応力を算定する場合,きっといろいろなモデルが
存在し得るのではあろうが,一つの基礎的なモデルは,
式(12.72)の加算則が成立することから何らかの
応力速度を
![]() と定義した上で
と定義した上で
のように弾性の構成則も増分で規定することだろう。章-9では,
そのような考え方で弾性も含めた増分理論を展開した。
そこで,物体と一緒に何らかの規則で回転した座標で
定義する客観性を持つ応力速度
![]() を
いくつか定義しよう。
を
いくつか定義しよう。
まず,客観性という言葉の意味をやや文学的に説明しておこう。
極分解の定理で回転![]() を除去された変形勾配成分である
変形テンソルが,材料が実際に感じている歪ゆがみであった。
これに対応した応力は,この歪みに相当する材料の抵抗力であり,
材料の抵抗則を表現するための数学的概念である。
変形速度にも,この回転
を除去された変形勾配成分である
変形テンソルが,材料が実際に感じている歪ゆがみであった。
これに対応した応力は,この歪みに相当する材料の抵抗力であり,
材料の抵抗則を表現するための数学的概念である。
変形速度にも,この回転
![]() は
含まれていなかったことを思い出して欲しい。
そこで応力速度を材料の抵抗力の表現として使うことを考えると,
物体と一緒に回転しながら実質的な歪みに対応する,
まさにLagrange的な尺度の方を用いるのが適切である。
例えば,物体に埋め込んだ座標と一緒に変化する第2 Piola-Kirchhoff応力の
変化率
は
含まれていなかったことを思い出して欲しい。
そこで応力速度を材料の抵抗力の表現として使うことを考えると,
物体と一緒に回転しながら実質的な歪みに対応する,
まさにLagrange的な尺度の方を用いるのが適切である。
例えば,物体に埋め込んだ座標と一緒に変化する第2 Piola-Kirchhoff応力の
変化率![]() は,その代表だろう。
しかし,後述の例のように,第2 Piola-Kirchhoff応力で
初期配置から破壊までの有限変形を追跡できるようなモデルを
作るのは困難だと予想される。
また,塑性は現配置からの接線的な抵抗則であることから,Lagrange的な
尺度の中でもどちらかと言うと節-12.4で
説明するupdated Lagrange的な尺度を用いた方がいいと思われる。
は,その代表だろう。
しかし,後述の例のように,第2 Piola-Kirchhoff応力で
初期配置から破壊までの有限変形を追跡できるようなモデルを
作るのは困難だと予想される。
また,塑性は現配置からの接線的な抵抗則であることから,Lagrange的な
尺度の中でもどちらかと言うと節-12.4で
説明するupdated Lagrange的な尺度を用いた方がいいと思われる。
そういった点を考慮すると,Euler的なCauchy応力やKirchhoff応力を用いる場合も,
接線的な構成則を定義する方が
材料試験結果をモデル化する場合に便利だと考えられる。
では,真応力と呼ばれているCauchy応力の時間変化率が持つ特性を,
回転している物体を例に用いて,示してみよう。図-12.11に
示したのは,一定応力![]() で抵抗している棒が,
速度
で抵抗している棒が,
速度![]() で回転している状態12.18である。
時刻
で回転している状態12.18である。
時刻![]() に棒が水平だったとすると,
この物体中のCauchy応力は座標変換の式(3.37)から
に棒が水平だったとすると,
この物体中のCauchy応力は座標変換の式(3.37)から
になるのは明らかである。応力は一様(一定)なので,
この物質微分は時間微分と同じになる(移流項は無くなる)ので
となり,いずれも零にはならない。 しかし,材料は常に一定の応力で抵抗したままであるから, 構成則に使われる応力速度は零であり続けなければならない。 だって材料は,回っていることには気付いていたとしても, 抵抗の仕方については何も変化を感じていないはずだからだ。 したがって,Cauchy応力の単純な物質微分は, 構成則には用いることができないことになる。 初学者はまずとても驚いて欲しいところだ。
そこで,物体と一緒に運動する系から見た応力の変化率を考えてみる。
まず物体に現配置で埋め込んだ座標を![]() とし,時刻
とし,時刻![]() には
これが空間固定座標に一致しているものとする。つまり
には
これが空間固定座標に一致しているものとする。つまり
とする。ある微分線要素![]() の変化をこの埋め込み座標から眺めると
の変化をこの埋め込み座標から眺めると
とみなすことができるが,![]() は物体に貼り付けてあるので
は物体に貼り付けてあるので
が成立するので,上式は
と書いてもいい。したがって,その逆関係から
と求められる。
つまりこの右辺の括弧は,時刻![]() における
空間固定座標系と埋め込み座標系との間の一種の座標変換行列になっている。
ところで,あとで証明するがCauchy応力は
における
空間固定座標系と埋め込み座標系との間の一種の座標変換行列になっている。
ところで,あとで証明するがCauchy応力は
のように更新できる。
そこで埋め込み座標で眺めたCauchy応力は,上の座標変換則を2階の
テンソルに拡張すれば
のように算出すればいいので,
これに上式を代入して![]() の1次項までを残すと
の1次項までを残すと
となる。時刻![]() には
には
![]() なので,
これからCauchy応力の埋め込み座標変化率を
なので,
これからCauchy応力の埋め込み座標変化率を
と定義できる。そこで図-12.11の回転する物体の
例で算定してみよう。この図の運動は
であるから,これと式(12.110) (12.111)を
式(12.112)に代入すると,すべて
となるので,抵抗の仕方が何も変化していないと材料が感じているということを
この応力速度
![]() は表現できたことになる。
このような応力速度は客観性を有していると呼ばれる。
この応力速度
は表現できたことになる。
このような応力速度は客観性を有していると呼ばれる。
この応力速度
![]() はOldroydの応力速度
とも呼ばれる。
はOldroydの応力速度
とも呼ばれる。
最もよく用いられるJaumannの応力速度は,やはり物体と一緒に運動する
座標から定義した速度であるが,変形しない埋め込み座標から観察した
速度である。
したがってそれは,上式(12.112)で速度勾配![]() から
変形速度
から
変形速度![]() を取り去ってスピン
を取り去ってスピン![]() だけにした
だけにした
で定義される。これがJaumannの応力速度
と呼ばれる応力速度であり,共回転応力速度
とも呼ばれ,これも客観性を有する応力速度である。
ただこの速度は,大きく伸びながら60度以上の角変化を
生じさせるような単純せん断において,正弦曲線のような応力ひずみ関係を
予測[49]してしまう(図-12.21にも
示した)等,使用には注意が必要である。
このように,種々の特性を持つ,客観性を有する応力速度は無数に定義でき,
構成則を定義するのに果たしてどれを用いたらいいのかの判断は難しいと
言われている。
ちなみにKirchhoff応力のJaumann速度
![]() は
は
と定義されている。
正統的な客観性の証明についてはとても数学的過ぎるので,
別途各種文献を眺めて欲しい。
文献[51]も比較的理解し易い。
実は,客観的な応力速度は無数に定義できる。
また,Cauchy応力![]() と変形速度
と変形速度![]() は客観性を有しているが,
それ以外のほとんどの各種変形や変形率は
客観性を持たないことには注意が必要である。
は客観性を有しているが,
それ以外のほとんどの各種変形や変形率は
客観性を持たないことには注意が必要である。