• • • 4.3.0.0.1 不静定梁と静定基本系:
    • 4.3.0.0.2 両端固定梁の場合:
    • 4.3.0.0.3 連続梁:
    • 4.3.0.0.4 弾性支持された片持ち梁:

4.3 重ね合わせの原理で不静定梁を解く

この節では，実際に現場で応力計算をするために必要な情報を 並べるのではなく，あくまでも物理現象をモデル化したあとの 問題解決の方法について，特に線形系の重ね合わせの原理 について概説する。 つまり，静定梁の解がわかっているものとして， それを用いて重ね合わせの原理で不静定構造を解く。 基本は，元の不静定構造を複数の静定構造に切断分解することから始める。 そうした上で，その切断箇所に必要な（未知な）不静定反力 を載せることによって，元の不静定構造と等価にする条件を導き出す。 この条件は，章-2の最後の3点で支持された剛棒の例で 述べたような，変形も含めた幾何学的な整合性を表す条件に相当する。 それを解くことによって不静定反力を求めるのだ。 この方法は，前節のように微分方程式を力任せに解くよりも楽に問題解決に 導いてくれることが多い。 また，静定系を重ね合わせて元の不静定構造を復元する際に 力学的な感覚が必要になる。そういう意味では極めて力学的な解法である。 不静定構造の問題に直面したときには，まず検討して欲しい大切な手法の一つである。

4.3.0.0.1 不静定梁と静定基本系:

図 4.39: 不静定梁を静定梁の重ね合わせで解く

最初に図-4.39に あるような基本的な不静定構造を解いてみる。 図示したように，これを二つの 静定系の重ね合わせとして考えるアプローチを2種類くらいは 思い付くのではないだろうか。 ここでは一つ目のアプローチを使ってみよう。 この重ね合わせは，左端に発生する不静定外力モーメントを 未知の$C_0$として二つの単純支持梁（静定基本系）に分解し， その重ね合わせが元の不静定系の境界条件を満足する ように$C_0$を決める方法である。 この$C_0$が不静定反力と呼ばれるものに相当する。 元に戻す条件である幾何学的な整合性は左端のたわみ角の等価性になる。 またこの図の二つ目の方法では，支点反力の$Q_0$が不静定反力であり， 整合性は右端のたわみの等価性である。

図 4.40: 重ね合わせで不静定系を解く例

静定系の左の系の左端のたわみ回転角は式(4.35)で 求められており，図に示した回転角は

$$\beta_A=w'(0)=\dfrac{q_0\ell^3}{24EI}$$

である。一方，右側の系の左端のたわみ角も式(4.39)で 求められており

$$\beta_B=-w'(0)=\dfrac{C_0\ell}{3EI}$$

となっている。この二つの系を重ねて元の系に等しくなるためには， 左端が固定端であることから，この二つの回転角が 等しくなければならない。つまり図にも示したように

$$\beta_A=\beta_B \quad\to\quad \dfrac{q_0\ell^3}{24EI}=\dfrac{C_0\ell}{3EI}$$

になるように$C_0$を決定すればいい。したがって

$$C_0=\dfrac{q_0\ell^2}{8}$$

となる。 それぞれの静定系の曲げモーメント図も，左側は2次曲線，右側は 線形とわかっているので，その重ね合わせにより正しい分布図を 描くことができる。曲げモーメント図に関して このようにして重ね合わせたものを図-4.40に示した。 不静定モーメント$C_0$を決めることができたから，たわみやたわみ角の 分布も二つの静定系の結果の重ね合わせで算定できる。

図 4.41: 重ね合わせで両端固定梁を解く

4.3.0.0.2 両端固定梁の場合:

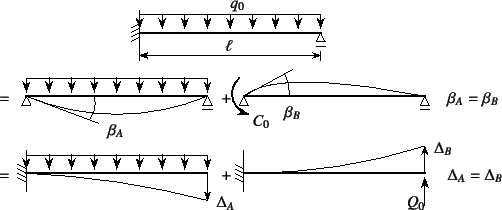
次の 例題は図-4.41の両端固定の 場合であるが，この場合にも例えば図示したような三つの静定系の 重ね合わせで解けそうだ。$C_1$と$C_2$が未知の不静定反力である。 等分布外力が作用した梁の 場合には，式(4.35)より

$$\beta_A\super{(l)}=w'(0)=\beta_A\super{(r)}=-w'(\ell) =\dfrac{q_0\ell^3}{24EI}$$

である。その次の左端に集中曲げ外力モーメントが作用した梁は， 式(4.39)に解があり

$$\beta_B\super{(l)}=-w'(0)=\dfrac{C_1\ell}{3EI},\quad \beta_B\super{(r)}=w'(\ell)=\dfrac{C_1\ell}{6EI}$$

となっていた。最後の右端に集中曲げ外力モーメントが 作用した梁の場合は上の逆であり，これは式(4.43)の 外力の向きを逆にした$C_0=-C_2$の場合に相当するから

$$\beta_C\super{(l)}=-w'(0)=\dfrac{C_2\ell}{6EI},\quad \beta_C\super{(r)}=w'(\ell)=\dfrac{C_2\ell}{3EI}$$

で与えられる。以上の三つの系を重ね合わせた結果が元の両端 固定梁になるためには，重ね合わせた系の両端のたわみ角が零になって いればいい。つまり

$$\beta_A\super{(l)} = \beta_B\super{(l)}+\beta_C\super{(l)} \... ...rac{q_0\ell^3}{24EI}=\dfrac{C_1\ell}{6EI}+\dfrac{C_2\ell}{3EI}$$

を満足するように$C_1$, $C_2$が決定されればいい。したがって

$$\left(\begin{array}{cc} 8 & 4 4 & 8 \end{array}\right) \... ...ell^2}{12} \left\{\begin{array}{c} 1 1 \end{array}\right\}$$

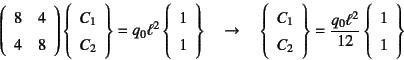
と端部の不静定モーメントを得る。 曲げモーメント図に関して このようにして重ね合わせたものを図-4.42に 示した。二つの不静定モーメント$C_1$, $C_2$が求められたので， たわみやたわみ角の分布も三つの静定系のそれぞれの結果の 重ね合わせによって算定できる。

図 4.42: 両端固定梁を重ね合わせで解く

4.3.0.0.3 連続梁:

次の 例題は図-4.43の2径間連続梁であるが， 境界値問題として微分方程式を解く正攻法が面倒だったため， その手順のみを示して解くのを 諦めた例題（4.31）であった。 この場合には，例えば図示したような二つの静定系に分けて 連続部分でたわみ角を整合させるようにしたらよさそうだ。 この左右のスパンそれぞれでも二つの外力条件に対する解の 重ね合わせで答を求めることができる。$C_0$が不静定反力である。

図 4.43: 連続梁を重ね合わせで解く例題

左半分の梁の右端の回転角は式(4.35)と 式(4.43)の重ね合わせで計算することができ

$$\beta_A=\dfrac{q_0\ell^3}{24EI}-\dfrac{C_0\ell}{3EI}$$

となる。一方，右半分の梁の左端の回転角は， 式(4.50)を1回微分したものと式(4.39)から

$$\beta_B=-\dfrac{Q\ell^2}{16EI}+\dfrac{C_0\ell}{3EI}$$

を得る。この二つを等置することによって

$$C_0=\dfrac{3Q\ell}{32}+\dfrac{q_0\ell^2}{16}$$

と中間支点上での不静定モーメントを求めることができる。

図 4.44: 重ね合わせで解く連続梁の曲げモーメント

あとは，この結果をそれぞれのスパンの静定解に代入してやれば 曲げモーメント図もたわみ形状も求められる。 結果を図-4.44に示した。 この連続梁の場合も1スパンの不静定梁と同様，中間載荷点および 支点部での不静定モーメントが求められさえすれば，モーメント分布は， 静定基本系のそれの重ね合わせによって求められることが 明らかになった。 したがって，この不静定モーメントを求めることが不静定梁を解く 場合の最初の目的と考えてもいいかもしれない。 そのためには章-5の方法が有効である。

4.3.0.0.4 弾性支持された片持ち梁:

図-4.21の 弾性支持された片持ち梁を重ね合わせの原理で解いてみよう。 この場合には，図-4.45にも示したように バネの接続点で切断して二つの系に分けて考えると簡単である。$X$が 未知の不静定反力である。 まず梁の先端のたわみを$\Delta$とすると， 式(4.42)と式(4.37a)の 重ね合わせから

$$\Delta=\dfrac{q_0\ell^4}{8EI}-\dfrac{X\ell^3}{3EI}$$

と表すことができる。

図 4.45: 弾性支持された片持ち梁

一方バネの縮みも$\Delta$であるから

$$X=k \Delta$$

という関係を満足している。この2式から$X$を消去すると

$$\Delta=\dfrac{3q_0\ell^4}{8EI\left(3+\alpha_s\right)}$$

と式(4.41)のパラメータ$\alpha_s$を 用いて解を得，これは式(4.40)に一致する。

図 4.46: 重ね合わせの演習問題
図 4.47: バネ支持された梁の問題

1. 図-4.39の二つ目のアプローチで同じ結果を 得ることができることを示せ。
2. 演習問題9で 解いた図-4.32(b)の系を重ね合わせで解け。
3. 図-4.43の連続梁を，中央支点の支承をはずす 代わりにその反力を不静定反力$X$として解け。
4. 図-4.46の 不静定梁の曲げモーメント分布を 静定系の重ね合わせで求めよ。二通りのアプローチを考えよ。
5. 図-4.47の系は，二つの 片持ち梁の先端同士を線形バネで結合したものである。 これを三つの系に分け，それぞれの梁の先端のたわみを求めよ。