7.6 ねじりを受ける棒の剛性方程式

章-5の有限要素法を用いて曲げねじりの剛性方程式を誘導しよう。ねじり角 $\varphi(x)$ で表したつり合い式が式(7.50)で与えられているので，長さ $\ell$ の棒の基本的な弱形式はまず

$\begin{displaymath} -\int_0^\ell \left\{-EI_\omega \varphi''''(x)+GJ \varphi''(x)\right\} \delta\varphi(x)\dint x=0 \end{displaymath}$

と表現できる。被積分関数の第1, 2項に関する積分をそれぞれ2回あるいは1回部分積分することによって，式(7.51)の境界条件を取り込んでいくことができ，最終的な仮想仕事の式が

$\begin{displaymath} EI_\omega\int_0^\ell \varphi'' \delta \varphi''\dint x +GJ... ...1 -(C_x)_2 \delta \varphi_2-(C_\omega)_2 \delta\gamma_2 = 0 \end{displaymath}$

(7.68)

と表現できる。ただし，簡単のために端部のそりを代表する変位成分を

$\begin{displaymath} \gamma_1\equiv -\varphi'(0), \quad \gamma_2\equiv -\varphi'(\ell) \end{displaymath}$

と置いた。式(7.68)の表現および境界条件から判断して，ねじり角 $\varphi(x)$ に仮定する変位関数は梁の曲げの問題と同様の3次の多項式でいいことがわかる。すなわち，式(5.21)の関数 $\psi_n(x)$ を用いて

$\begin{displaymath} \varphi(x)\sim\varphi_1 \psi_1(x)+\gamma_1 \psi_2(x)+ \varphi_2 \psi_3(x)+\gamma_2 \psi_4(x) \end{displaymath}$

(7.69)

これを仮想仕事式(7.68)に代入して有限要素定式化の標準手順を踏んでもいいが，この曲げねじり問題と章-6の梁-柱の問題とはその表現が非常によく似ていることに気付く。一般解が双曲線関数か三角関数かの違いがあるように，微分方程式の係数の符号の違いで解の性質は全く違ってしまっているが，有限要素定式化の観点から式(7.50) (7.51)と式(6.30) (6.31)とを比較すると

$\begin{displaymath} (w,\theta)\leftrightarrow (\varphi,\gamma), \quad (EI,P)\l... ... q\leftrightarrow 0, \quad (S,C)\leftrightarrow (C_x,C_\omega) \end{displaymath}$

の置き換えによって二つの問題の表現には一対一の対応があることがわかる。したがって式(7.69)を式(7.68)に代入して演算を続行するまでもなく，曲げねじり問題の剛性方程式は式(6.58)を参考にして

$\begin{displaymath} \left\{\begin{array}{c}(C_x)_1 (C_\omega)_1\\ (C_x)_2 ... ...arphi_1 \gamma_1\\ \varphi_2 \gamma_2\end{array}\right\} \end{displaymath}$

(7.70)

となることが明らかである。なお簡単のためにこの章では，括弧無しの太字で行列を表している。ここに

$\begin{displaymath} \fat{k}_\omega \equiv \mat{\left(k_\omega\right)_{ij}}, \qua... ...ad (k_S)_{ij}\equiv GJ \int_0^\ell \psi'_i \psi'_j\dint x\end{displaymath}$

(7.71)

で定義された剛性行列はそれぞれ，曲げねじりに関するものとSaint-Venantのねじりに関するものとに相当する。行列の具体的な表現はそれぞれ，式(5.24)の初等梁の曲げ剛性行列と式(6.59)の幾何剛性行列とに対応しており

$\begin{displaymath} \fat{k}_\omega=EI_\omega \left(\begin{array}{@{}cccc@{}} \d... ...umn{3}{l}{\mbox{Symm.}} & \dfrac{2\ell}{15} \end{array}\right) \end{displaymath}$

(7.72)

となっている。なお簡単のために，この章では括弧無しの太字で行列を表している。

もちろん前の例題で見たように $\varphi(x)$ の一般解は双曲線関数なので，梁や柱の問題とは異なり，有限要素法による解は節点においても正解には一致しない近似になる。ただ近似度については梁-柱と同程度であり，梁-柱の座屈問題の数値解の例からも明らかなように，比較的少ない要素分割でも工学的には十分な精度で近似解を求めることができる。

7.6.2 Saint-Venantのねじり問題

図-7.30でも示したように，一般に細長い構造棒部材では曲げねじり成分がそれほど大きな影響を及ぼさない場合も多い。その場合，式(7.70)の剛性方程式の第2, 4行目左辺の曲げねじりモーメントは常に零である上に，要素間でねじり率 $(-\varphi')$ は連続する必要は無く^7.4なる。したがって，この左辺が零の第2, 4行の式は各要素毎の剛性方程式への局所的な拘束条件であり，全体系の剛性方程式に重ねてはいけない。つまりこの2式は個々の要素で独立して成立すべき条件で，それは両端の $\varphi_i$ と $\gamma_i$ の間の制約条件を与えている。結局この2行の式を $\gamma_i$ について解くと，

も $EI_\omega$ も消え去り

$\begin{displaymath} \left\{\begin{array}{c} \gamma_1 \gamma_2 \end{array}\rig... ...t\{\begin{array}{c} \varphi_1 \varphi_2 \end{array}\right\} \end{displaymath}$

(7.73)

となる。この式は，ねじり率を両端のねじり角の差で表したものであり，後述のように $\varphi$ に1次多項式を仮定してねじり率 $\gamma$ を算定したものと同じである。この関係を元の要素剛性方程式(7.70)の第1, 3行に代入することによって剛性行列の縮約が行われ，最終的な要素剛性方程式が

$\begin{displaymath} \left\{\begin{array}{c} (C_x)_1 (C_x)_2 \end{array}\right... ...t\{\begin{array}{c} \varphi_1 \varphi_2 \end{array}\right\} \end{displaymath}$

(7.74)

となる。行列の縮約という操作によって自動的に $EI_\omega$ の項がすべて消え去っているのは興味深い[30]。すなわち，Saint-Venantのねじりだけを考慮すればいい場合の棒は，ちょうどバネ定数が $(\slfrac{GJ}{\ell})$ の線形バネとしてねじり外力に抵抗していると考えればいい。

もちろん式(7.74)の剛性方程式は，式(7.6)で表されたSaint-Venantのねじりモーメントのつり合い式と境界条件式(7.8)とから求められる弱形式

$\begin{displaymath} \int_0^\ell GJ\varphi' \delta \varphi'\dint x -(C_x)_1 \delta \varphi_1-(C_x)_2 \delta \varphi_2 = 0 \end{displaymath}$

からも誘導できる。この形式は式(5.13)の柱の仮想仕事式の分布外力項を無視したものに一致しているから，仮定する変位関数も柱の場合と同様1次の多項式でいいことがわかり，式(5.15)の関数 $\phi_i(x)$ を用いて

$\begin{displaymath} \varphi(x)=\varphi_1 \phi_1(x)+\varphi_2 \phi_2(x) \end{displaymath}$

と置けばいい。これを上の仮想仕事式に代入すれば上式(7.74)の剛性方程式を求めることができる。またSaint-Venantのねじりのみの場合に，節点のねじり角 $\varphi_i$ が厳密解に一致するのは，柱の場合と同じである。

7.6.3 立体骨組の問題

7.6.3.1 簡単な例題

**図 7.35:** 二つの円柱が作る簡単な立体構造
$\begin{figure}\begin{center} \unitlength=.25mm \begin{picture}(387,123)(49,-5)... ...put(368,-1){{\xpt\rm$\slfrac{Q_0}{2}$}} % \end{picture}\end{center} \end{figure}$

ねじり変形が生じない平面骨組の問題は，例えば式(5.32)の剛性方程式で

面内の問題を解決できる。これが現実の構造系のように立体骨組である場合には，

面内と

面内での軸力と2軸回りの曲げを受ける平面問題の剛性方程式に，ねじり抵抗に関する剛性方程式を加えてやれば，その解析が可能になりそうだ。まず，答を確かめ易いように，剛性方程式を用いないで済むような簡単な例題を一つ解いておこう。

図-7.35の左図の問題では，せん断外力の影響で片方の棒がたわんで先端にたわみ角が生じるが，それをもう片方の棒のねじり抵抗も部分的に拘束している。したがって右図のようにそれぞれの棒を分離し，それぞれの棒の先端に他方からのねじり抵抗に相当する集中外力モーメント

が，不静定モーメントとして作用していると考えればいい。載荷点に対して対称構造であることから，せん断外力は半分ずつそれぞれの片持ち棒に作用していると考えていいし，上の不静定モーメントもすべて同じ値になる。まず左手前の棒の曲げを考えると，その曲げによる先端のたわみ角は，式(4.37b)および式(4.38)から

$\begin{displaymath} -w'(\ell)=(\mbox{$y$軸右ねじ方向のたわみ角})= -\dfrac{\slfrac{Q_0}{2}\ell^2}{2EI}+\dfrac{C_0\ell}{EI} \end{displaymath}$

の値を持つ。一方ねじり抵抗は，円柱の場合にはSaint-Venantのねじりだけでいいので，式(7.9a)で得た結果から右奥の棒側の先端のねじり回転角は

$\begin{displaymath} \varphi(\ell)=(\mbox{$y$軸右ねじ方向のねじり角})=-\dfrac{C_0\ell}{GJ} \end{displaymath}$

となる。この場合の先端での幾何学的な整合性あるいは連続性は，片方の棒のねじり回転角がもう片方のたわみ角に等しくならなければならないことを要請する。したがって，以上の二つの式を等値して

$\begin{displaymath} -\dfrac{\slfrac{Q_0}{2}\ell^2}{2EI}+\dfrac{C_0\ell}{EI}= -\... ...c{C_0\ell}{GJ} \quad\to\quad C_0=\dfrac{Q_0\ell GJ}{4(GJ+EI)} \end{displaymath}$

のように不静定モーメントが求められる。よって，例えば左手前の棒の場合には

$\begin{displaymath} \varphi(x)=-\dfrac{Q_0\ell x}{4(GJ+EI)}, \quad w(x)=\dfrac{Q_0\ell(GJ+2EI)}{8EI(GJ+EI)}x^2-\dfrac{Q_0}{12EI}x^3 \end{displaymath}$

(7.75)

というねじり角とたわみの分布を示す。

の極端な場合には，先端にせん断外力 $\slfrac{Q}{2}$ が作用した1本の片持ち梁の曲げの解を得ることができる。

7.6.3.2 要素座標系での要素剛性方程式

上の例題のような簡単な場合を除けば，境界値問題を直接解いたり静定基本系の重ね合わせを行うより，剛性方程式を用いた方が実用的であろう。そのときに気になるのは，曲げや軸力に関する剛性方程式とねじりに関する剛性方程式との連成作用である。長方形断面を例に簡単に議論してみよう。

式(7.22)で得た

方向の変位成分は，新しく導入された単位そりを用いれば

$\begin{displaymath} u_x(x,y,z)=u(x)-\omega(y,z) \varphi'(x), \qquad \omega(y,z)=yz_s-zy_s-yz \end{displaymath}$

と表現できる。

は図心で定義された

方向変位である。一方，曲げと軸力を受ける棒の場合の軸方向の変位成分は，式(4.3a)を

平面内の曲げにも拡張することによって

と表すことができる。ここに

と

はそれぞれ

方向の断面の変位成分で，二つ共せん断中心Sで定義されているものとする。したがって，軸力・曲げとねじりを同時に受ける部材の軸方向変位成分は

$\begin{displaymath} u_x(x,y,z)=u(x)-z w'(x)-y v'(x)-\omega(y,z) \varphi'(x) \end{displaymath}$

(7.76)

$\begin{displaymath} \sigma_{xx}(x,y,z)= E\left\{ u'(x)-z w''(x)-y v''(x)-\omega(y,z) \varphi''(x) \right\} \end{displaymath}$

(7.77)

$\begin{displaymath} M_z(x)=EJ_zu'-EI_zw''-EI_{yz}v''-EI_{\omega z}\varphi'' \end{displaymath}$

$\begin{shorteqns} J_y & \equiv & \int_A y\dint A, \quad \EQsep J_\omega\equiv\... ...dint A, \quad \EQsep I_{\omega y}\equiv\int_A \omega y\dint A \end{shorteqns}$

(7.78)

と定義してある。 $I_{yz}$ は断面相乗モーメント と呼ばれている。さらに，式(7.56)に式(7.77)を代入することによって，曲げねじりモーメントは

$\begin{displaymath} M_\omega(x)=EJ_\omega u'-EI_{\omega z}w''-EI_{\omega y}v'' -EI_\omega \varphi'' \end{displaymath}$

となる。このように立体構造の場合には，変位の微係数で表された変形と断面力の関係がお互いに連成し合い，例えば平面問題の式(4.13)のようには分離できていない。

しかし章-4でも示したように，原点を図心に選んでやれば

に関する断面1次モーメント

を零にできる。さらに，断面相乗モーメントも

を満足するように

軸を設定することも可能である。このように選ばれた

軸を断面の主軸 と呼ぶ。さらに，式(7.60) (7.61)を満足するようにせん断中心と $\omega_c$ を定義することが可能であることから，断面力と変位成分との関係はすべて独立になり

$\begin{displaymath} N = EA u', \quad M_z=-EI_z w'', \quad M_\omega=-EI_\omega... ...i'', \quad M_y \equiv \int_A \sigma_{xx} y \dint A=-EI_y v'' \end{displaymath}$

と関係付けることが可能である。

は式(7.78d)で定義されている。

以上のように変位成分を定義する位置を適切に設定しておけば，立体骨組の剛性方程式は，平面骨組のそれとねじりに関する剛性方程式とを単純に併記すればいいことになる。まず節点の変位成分を

$\begin{displaymath} \fat{u}_i\equiv\lfloor u_i\;\; v_i\;\; w_i\;\; \varphi_i\;\... ...'_i\;\; v'_i\;\; \gamma_i \rfloor\supersc{t} \qquad (i=1,2) \end{displaymath}$

(7.79)

と定義する。

に負の符号が付いていないのは，

が

軸右ねじ方向のたわみ角になって通常の外力モーメントの正の向きと一致するからである。これに対応させて，外力成分も

$\begin{displaymath} \fat{f}_i\equiv\lfloor F_i\;\; {S_y}_i\;\; {S_z}_i\;\; {C_x... ... {C_y}_i\;\; {C_\omega}_i \rfloor\supersc{t} \qquad (i=1,2) \end{displaymath}$

(7.80)

と定義する。ここに ${S_z}_i$ , ${C_z}_i$ は章-5で定義した

の下添え記号を書き換えただけのものであり，したがって ${S_y}_i$ , ${C_y}_i$ は

方向のせん断外力と

軸右ねじ回りの曲げ外力モーメントである。式(7.80)の外力成分は，外力仮想仕事項で式(7.79)の変位成分と仕事をする対となる外力である。軸力と2軸回りの曲げ外力モーメントは図心に，せん断外力とねじりに関する外力モーメントはせん断中心に作用しているものとする。簡単のために分布外力項を省略してしまうと，立体骨組の要素剛性方程式は上の記号を用いて

$\begin{displaymath} \left\{\begin{array}{c} \fat{f}_1 \fat{f}_2 \end{array}\r... ...t\{\begin{array}{c} \fat{u}_1 \fat{u}_2 \end{array}\right\} \end{displaymath}$

(7.81)

と表される。ここに $\fat{k}_s\supersc{x}$ (X=A, B, C)は，立体骨組の剛性行列をそれぞれ $7\times 7$ の小行列に分割したもので，具体的には

$\begin{displaymath} \fat{k}_s\supersc{a} = \left(\begin{array}{@{}c@{}c@{}c@{}c@... ...ac{2EI_\omega}{\ell}\!-\!\frac{\ell GJ}{30} \end{array}\right) \end{displaymath}$

(7.82)

のような表現になる。 $\fat{k}_s\supersc{c}$ は $\fat{k}_s\supersc{a}$ の非対角項のみの符号を変えた行列である。部材長が比較的長い場合等のように，そりを無視する場合には， $\gamma_i$ を消去した式(7.74)の方を重ねればいい。そのため，節点変位・節点外力ベクトルは $\gamma_i$ , ${C_\omega}_i$ の無い6行になるから

$\begin{displaymath} \fat{k}_s\supersc{a}\!=\!\left(\begin{array}% {@{}c@{\!\!\!... ...}{\ell^2} & 0 & 0 & 0 & \frac{2EI_y}{\ell} \end{array}\right) \end{displaymath}$

(7.83)

7.6.3.3 隣り合う要素の断面形状が異なる場合

**図 7.36:** 変位と外力の定義された点を一般化する
$\begin{figure} % latex2html id marker 30098 \begin{center} \unitlength=.25mm \be... ...\put(184,-1){{\xpt\rm$\Rightarrow$}} % \end{picture}\end{center}% % \end{figure}$

しかしながら一般に，それぞれの部材は，それが主にどんな抵抗力を期待されているかによって全く異なる断面形状を有している。そのような相異なる断面を持つ部材で構成された立体骨組では，部材の接合点で図心同士あるいはせん断中心同士が同一点を通過するように配置できるとは限らない。したがって，上の要素剛性方程式を直接剛性法で単純に重ね合わせることはできないのが普通である。また一方で，もしコンピュータで剛性方程式を解くのであれば，曲げと圧縮やねじりとを独立させる必要性はほとんど無く，変位や力のベクトル成分を敢えて図心等で定義しておく必要は無くなる。

したがって例えば，折れ曲がってもいいが連続した線で全部材の軸線方向に沿った部材骨格を表す線（以下「骨格線」と呼ぶ）を一巡り定義し，各部材毎にこの骨格線が通過する断面内の点A

を決め，その点で剛性方程式の外力ベクトル成分や変位ベクトル成分を定義するように剛性方程式を変更すれば，直接剛性法が使えて便利になる。詳細については参考文献[118,125,126]等を参照して欲しいが，式(7.79) (7.80)の変位ベクトル成分および外力ベクトル成分の代わりに，任意点Aですべての成分を定義したベクトル $\widetilde{\fat{u}}_i$ , $\widetilde{\fat{f}}_i$ を定義し，剛性方程式(7.81)を

$\begin{displaymath} \left\{\begin{array}{c} \widetilde{\fat{f}}_1 \widetilde... ...etilde{\fat{u}}_1 \widetilde{\fat{u}}_2 \end{array}\right\} \end{displaymath}$

(7.84)

と表したい。図-7.36に式(7.81)の剛性方程式における各成分の定義された点と式(7.84)での定義とを対比させて表示しておいた。それぞれの成分同士には

$\begin{displaymath} \fat{u}_i=\fat{D}_u \widetilde{\fat{u}}_i, \quad \fat{f}_i=\fat{D}_f \widetilde{\fat{f}}_i \end{displaymath}$

$\begin{displaymath} \widetilde{\fat{k}}_s\supersc{x}\equiv \fat{D}_f^{-1} \fat... ..._s\supersc{x} \fat{D}_u \quad (\mbox{{\sc x}={\sc a, b, c}}) \end{displaymath}$

$\begin{displaymath} \fat{D}_u\supersc{t}=\fat{D}_f^{-1}, \quad \fat{D}_u^{-1}=\fat{D}_f\supersc{t} \end{displaymath}$

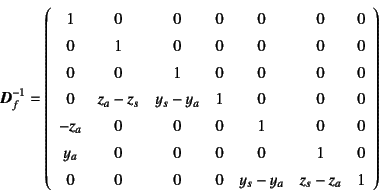
$\begin{displaymath} \fat{D}_f^{-1}= \left(\begin{array}{ccccccc} 1 & 0 & 0 & 0... ... 0 & 0 & 0 & 0 & y_s-y_a & z_s-z_a & 1 \\ \end{array}\right) \end{displaymath}$

と表される。こうすることによって，軸力や曲げおよびねじりに関する剛性方程式同士の連成は避けられなくなるものの，剛性方程式のベクトル成分がある連続した共通の骨格線上での物理量で定義されるため，異なる断面を持つ部材間の連続条件も簡単に表現でき，いわゆる直接剛性法がそのまま適用できる。そりを無視する場合には，上の行列の7列7行を無視した $6\times 6$ の行列を用いればいい。

各行列の陽な表現は， $\widetilde{\fat{k}}_s\supersc{x}= \fat{k}_s\supersc{x}+\Delta\fat{k}_s\supersc{x}$ と差分表示すると

$\displaystyle \Delta\fat{k}_s\supersc{a}$	$\textstyle =$	$\displaystyle \left(\begin{array}{@{}c@{ }c@{ }c@{}cccc@{}} 0 & 0 & 0 & 0 & -\f... ...rac{4E\widetilde{J_y}}{\ell}+\frac{4E\widetilde{J_z}}{\ell} \end{array}\right),$
			(7.85)
$\displaystyle \Delta\fat{k}_s\supersc{b}$	$\textstyle =$	$\displaystyle \left(\begin{array}% {@{}c@{\!\!\!}c@{ }c@{ }c@{ }c@{ }c@{ ... ...2E\widetilde{J_y}}{\ell}\! +\!\frac{2E\widetilde{J_z}}{\ell} \end{array}\right)$

となる。 $\Delta\fat{k}_s\supersc{c}$ は $\Delta\fat{k}_s\supersc{a}$ の括弧付きの項のみの符号を変えた行列である。ただし

$\begin{displaymath} \widetilde{I_y}\equiv (z_s-z_a) I_y, \qquad \widetilde{I_z}... ...z_s-z_a)^2 I_y, \qquad \widetilde{J_z}\equiv (y_s-y_a)^2 I_z \end{displaymath}$

7.6.3.4 全体座標系での剛性方程式と例題

直接剛性法がそのまま使えるように剛性方程式を修正したとしても，立体骨組の場合も平面骨組と同様それぞれの部材はそれぞれ異なる方向を向いているため，上の式(7.84)はそれぞれの要素の局所的な座標系における要素剛性方程式に過ぎなくなる。1要素の軸方向の要素座標を $\xi$ とし，それに直交する断面の主軸方向をそれぞれ $\eta$ , $\zeta$ 軸とする。これに対し，すべての要素に共通な全体座標系を(

)としておいて，この( $\xi$ , $\eta$ , $\zeta$ ) $\leftrightarrow$ (

)の間の座標変換行列 $\fat{T}_s$ を

$\begin{displaymath} \widetilde{\fat{u}}_i=\fat{T}_s \overline{\fat{u}}_i, \quad \widetilde{\fat{f}}_i=\fat{T}_s \overline{\fat{f}}_i \end{displaymath}$

(7.86)

と定義する。上棒付きの $\overline{\fat{u}}_i$ , $\overline{\fat{f}}_i$ が

全体座標系での成分である。これによって，すべての部材に共通する全体座標系での要素剛性方程式が平面骨組の式(5.38)と同様

$\begin{displaymath} \left\{\begin{array}{c} \overline{\fat{f}}_1 \\ \overline... ...rline{\fat{u}}_1 \\ \overline{\fat{u}}_2 \end{array}\right\} \end{displaymath}$

(7.87)

と表現できる。座標変換行列の一般的な表現には例えばEuler角を用いる等種々の方法があるが，詳細は参考文献を参照のこと。ここでは図-7.35の例題を，そりを無視した2要素の剛性方程式を用いて解き，式(7.75)の解析解と比較する。

**図 7.37:** 二つの円柱が作る簡単な立体構造の有限要素解析
$\begin{figure}\begin{center} \unitlength=.25mm \begin{picture}(211,111)(160,-5) ... ...7 (string) \put(252,-1){{\xpt\rm$Q_0$}} % \end{picture}\end{center} \end{figure}$

図-7.37にあるように

軸に平行な部材の両節点を1, 2として要素(1)と呼ぶ。これに対して，右側の部材の軸方向要素座標を $\xi$ ，それに直交する座標を図のように定義し，要素(2)と呼ぶ。要素(1)は要素座標と全体座標とが一致しているから座標変換行列は単位行列になる。一方，要素(2)の座標変換行列は

$\begin{displaymath} \fat{T}_s=\left(\begin{array}{ccc} \fat{T}_{ss} & \fat{0}_3... ...\fat{0}_3 \\ \fat{0}_3 & \fat{T}_{ss} \\ \end{array}\right) \end{displaymath}$

(7.88)

となる。ここで， $\fat{0}$ は3行の零ベクトル， $\fat{0}_3$ は $3\times 3$ の零行列であり

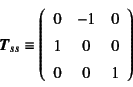
$\begin{displaymath} \fat{T}_{ss}\equiv \left(\begin{array}{ccc} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{array}\right) \end{displaymath}$

で定義される行列 $\fat{T}_{ss}$ が，この問題における全体座標系

から局所座標系 $(\xi,\eta,\zeta)$ へのベクトル成分の座標変換行列になっている。式(7.88)の右側の表現はそりを無視した $6\times 6$ の場合の座標変換行列である。

円柱では図心とせん断中心が一致しているので，この同じ2本の円柱部材に共通な骨格線も図心を通る線でいい。したがって，簡単のために剛性行列の上波線を省略し，そりも無視するから，以下の行列サイズは $6\times 6$ になる。要素(1)の全体座標系での要素剛性方程式は，式(7.87)の中の座標変換行列を取り除いたもので

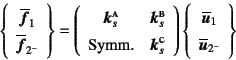
$\begin{displaymath} \left\{\begin{array}{c} \overline{\fat{f}}_1 \overline{\... ...ine{\fat{u}}_1 \overline{\fat{u}}_{2^-} \end{array}\right\} \end{displaymath}$

と表すことができる。一方要素(2)の方は，断面定数が要素(1)と同じなので同じ剛性行列の記号を使うと，上の座標変換行列を用いて

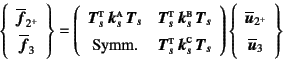
$\begin{displaymath} \left\{\begin{array}{c} \overline{\fat{f}}_{2^+} \overli... ...ine{\fat{u}}_{2^+} \overline{\fat{u}}_3 \end{array}\right\} \end{displaymath}$

となる。したがって直接剛性法がそのまま適用でき，全体剛性方程式は

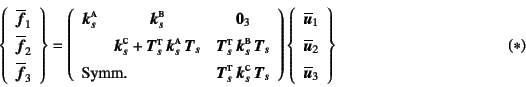
$\begin{displaymath} \left\{\begin{array}{c} \overline{\fat{f}}_1 \\ \overline... ...{u}}_2 \overline{\fat{u}}_3 \end{array}\right\} \eqno{(*)} \end{displaymath}$

となる。境界条件は節点の1と3とですべての変位を拘束しており

$\begin{displaymath} \overline{\fat{u}}_1=\fat{0}, \quad \overline{\fat{u}}_3=\fat{0} \end{displaymath}$

$\begin{displaymath} \overline{\fat{f}}_2= \lfloor 0\;\; 0\;\; Q_0\;\; 0\;\; 0\;\; 0 \rfloor\supersc{t} \end{displaymath}$

と与えられる。したがって，式(

)でまず解けるのは節点2に関する行であり，それは

$\begin{displaymath} \overline{\fat{f}}_2=\left( \fat{k}_s\supersc{c} +\fat{T}_... ...\fat{k}_s\supersc{a} \fat{T}_s \right) \overline{\fat{u}}_2 \end{displaymath}$

となる。そりを無視したときの具体的な $\fat{k}_s\supersc{a}$ , $\fat{k}_s\supersc{c}$ は式(7.83)を用いればよく，式(7.88)を用いると

$\begin{displaymath} \fat{T}_s\supersc{t} \fat{k}_s\supersc{a} \fat{T}_s= \lef... ...5}{l}{\mbox{Symm.}} & \slfrac{4EI_y}{\ell} \end{array}\right) \end{displaymath}$

となる。これを上の表現に代入し，外力

のある第3行と連成する行だけを取り出すと第3, 4, 5行目のみになり，それが

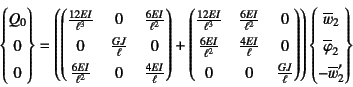
$\begin{displaymath} \left\{\begin{array}{@{}c@{}} Q_0 0 0 \end{array}\righ... ...\overline{\varphi}_2 \\ -\overline{w}'_2 \end{array}\right\} \end{displaymath}$

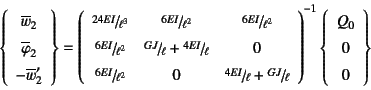
$\begin{displaymath} \left\{\begin{array}{c} \overline{w}_2 \overline{\varphi... ...{-1} \left\{\begin{array}{c} Q_0 0 0 \end{array}\right\} \end{displaymath}$

を解けばよく，行列式を計算して逆行列の第1列目の要素を算定すれば

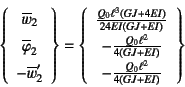
$\begin{displaymath} \left\{\begin{array}{c} \overline{w}_2 \overline{\varphi... ...4(GJ+EI)} \\ -\frac{Q_0\ell^2}{4(GJ+EI)} \end{array}\right\} \end{displaymath}$

が節点2の変位成分になる。これは式(7.75)の

に $\ell$ を代入した厳密解に一致している。残りの行は上の3行とは連成せず，左辺が零で剛性行列が正則なため対応する変位成分もすべて零になる。このように，解法そのものは平面骨組と同じなのでその詳細や他の例題については割愛するが，座標変換行列の算定法については参考文献等を必ず参照して欲しい。

近年，骨組の有限要素解析をする文献をあまり見ない。汎用プログラムが構造部材要素を有していないのかもしれない。ここではやや古典的な剛性方程式を誘導したが，弾塑性解析のことも念頭に置くと，断面1次モーメント等を零にして，曲げと軸力・ねじりを独立させる必要性も無くなる。そういう意味では，ここに説明したような有限要素解析は古いアプローチかもしれないので注意して欲しい。